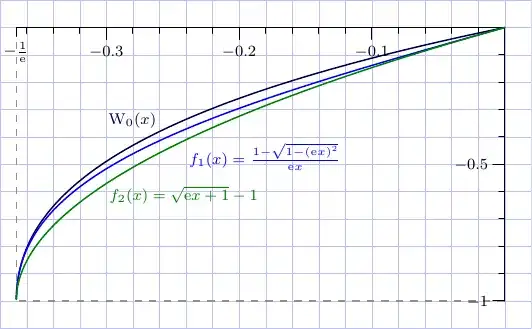
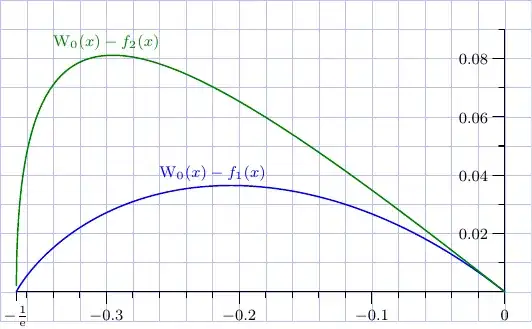
I want to find a lower bound for the branch $W_0(x)$ of Lambert $W$ function, for real values in range $-\frac{1}{e} \leq x \leq 0$. It is apparent that $-1$ is a lower bound for this function in the aforementioned range, but I need a slightly tighter lower bound.
Can anybody offer a better lower bound for this function using only elementary functions?