1

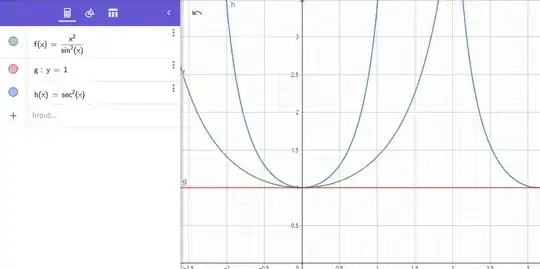
I know from L'Hopital's Rule that $$\lim_{t \to 0} \frac{t^2} {\sin^2(t)}=1$$

But I'm also trying to verify this using the Squeeze Theorem.

My first thought is to use the upper and lower bounds of possible outputs (range) of $\sin^2(t)$ as the functions which $\sin^2(t)$ would be between:

$$ 0 \leq \sin^2(t) \leq 1 $$

We want the function in the middle of the inequality to resemble the function we are taking the limit of, so dividing the whole inequality by $t^2$

$$0 \leq \frac{\sin^2(t)}{t^2} \leq \frac{1}{t^2}$$

Then taking the reciprocal of each term

$$0 \geq \frac{t^2}{\sin^2(t)} \geq t^2$$

Now taking the limit of each term of the inequality as $t \to 0$

$$\lim_{t \to 0} 0 \geq \lim_{t \to 0} \frac{t^2}{\sin^2(t)} \geq \lim_{t \to 0} t^2$$

$$ 0 \geq \lim_{t \to 0} \frac{t^2}{\sin^2(t)} \geq 0$$

Thus, by the Squeeze Theorem

$$\lim_{t \to 0} \frac{t^2}{\sin^2(t)} = 0$$

But I know this is incorrect and the limit should evaluate to $1$ just like the answer I got using L'Hopital's Rule. (And this can also be verified looking at the graph of $\frac{t^2}{\sin^2(t)}$ as $t \to 0$).

I'm not sure what step I did incorrectly or perhaps the functions I initially chose as the boundaries are incorrect.

So my questions are how would I evaluate this using the Squeeze Theorem and what part of my thought process is wrong?

Slecker
  • 969
  • 10
  • 29
  • 4
    You took the reciprocal of $0$ and got $0$! – copper.hat Sep 13 '20 at 01:00
  • 1
    You made a mistake when you took the reciprocal of each term. –  Sep 13 '20 at 01:01
  • @copper.hat Ah I see, so you mean I have $ 0 = \frac {0}{1}$ and taking its reciprocal I essentially got division by $0$ which is $\frac{1}{0}$ – Slecker Sep 13 '20 at 01:02
  • Who says you can use the squeeze theorem here? –  Sep 13 '20 at 01:04
  • @ChrisCuster Could you elaborate your comments in an answer. – Slecker Sep 13 '20 at 01:05
  • @ChrisCuster I wanted to see if it's possible. I did not think it wasn't possible to use the Squeeze Theorem. – Slecker Sep 13 '20 at 01:06
  • You probably can, come to think of it, since $\sin t\sim t$ for small $t$. –  Sep 13 '20 at 01:06
  • The issue with using the squeeze theorem is finding suitable bounds. Without resorting to derivatives, nothing obvious leaps out at me. – copper.hat Sep 13 '20 at 01:14
  • FYI: Knowing $\displaystyle{\lim_{x\to 0}\frac{\sin x}{x}}$ is equivalent to knowing the derivative of $\sin x$ at $x=0$: $$ 1=\lim_{x\to 0}\frac{\sin x}{x}=\lim_{x\to0}\frac{\sin x-\sin 0}{x-0}=\frac{d}{dx}\Bigg|_{x=0}\sin x. $$ So saying you know the limit from l'Hospital's rule is circular(ish) reasoning (and probably makes every calculus instructor sigh when they see it). – yoyo Sep 13 '20 at 01:50

3 Answers3

1

As stated in the comments, the reciprocal of zero isn't zero. Instead, apply the inequality derived here

$${t-\frac{t^3}{6} \le\sin (t)\le t},$$

which implies

$$ \frac{1}{t^2}\le \frac{1}{\sin^2(t)}\quad\text{and} \quad \frac{1}{\sin^2(t)}\le \frac{1}{\left(t-\frac{t^3}{6}\right)^2}.$$

Therefore

$$1 = \frac{t^2}{t^2}\le \frac{t^2}{\sin^2(t)}\le \frac{t^2}{\left(t-\frac{t^3}{6}\right)^2}=\frac{1}{\left(1-\frac{t^2}{6}\right)^2},$$

and taking the limit as $t\to 0$ gives the upper and lower bound of $1$ needed for the Squeeze theorem.

Axion004
  • 10,056
1

Try the following sandwich relation $$1<\frac{x^{2}}{\sin^{2}x}<\sec^{2}x$$

This easily gives you your desired limit.

Also, this relation can be graphically represented as follows

enter image description here

That's the sandwich :P

Soumyadwip Chanda
  • 1,506
1

$$\lim_{t\to 0} \frac{t^2}{\sin^2 (t)}=\lim_{t\to 0} \left(\frac{t}{\sin(t)}\right)^2$$ $$=\left(\lim_{t\to 0}\frac{\sin(t)}{t}\right)^{-2}=1^{-2}=1.$$ The limit $$\lim_{t\to 0}\operatorname{sinc}(t)=1$$ Can be verified with the squeeze theorem and has already been discussed at length on this site.

K.defaoite
  • 12,536