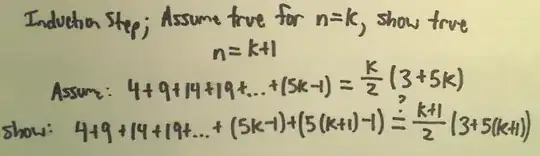2

Hi I wrote a formula to know the 100th term for the following sequence: $$3, 10, 17, 24, 31$$

Note that each following number in the sequence will be 7 more than the previous number.

And here is the formula: $$7N - 4$$ $$ \begin{array}{c|c} Term & 1 & 2 & 3 & 4 & 5 & Nth & 100 \\ \hline Number & 3 & 10 & 17 & 24 & 31 & 7\times N - 4 & 696 \\ \end{array} $$

I proved it with the base case $$5 \times 7 - 4 = 31$$

which is correct. And I proved it with$$100\times7 - 4 = 696,$$ which is correct.

Also I was looking at this induction example:

enter image description here

enter image description here

So that I can apply on my own induction. But the problem is I can't really apply it, because I don't know what to assume/claim to prove it. This is where I'm stuck:

$$ \mathrm{Induction \enspace step; \enspace Assume \enspace true \enspace for \enspace n=k, \enspace show \enspace true \enspace n=k+1} $$ $$ \mathrm{Assume: 3,10,17,24,...,[WHAT \enspace DO \enspace I \enspace NEED \enspace TO \enspace WRITE \enspace HERE?] = 7N-4} $$

Does someone has any idea what I need to write in the above assumption? Thanks in advance.

superkytoz
  • 131
  • 2
    what is the claim you want to prove? – Y.T. Sep 12 '20 at 16:43
  • 6
    I do not understand your question. You have a sequence which starts with $3,10,17,24,31$. That isn't enough information about the sequence... you only told us how the sequence started, but not how it continues. You want to prove that the rest of the entries in the sequence must necessarily fit the pattern that you propose? If all you told us was the start, that is impossible. There are uncountably infinitely many sequences who start that same way but do not continue the same pattern. – JMoravitz Sep 12 '20 at 16:46
  • 1
    Now... if you were to more adequately define the sequence and say "each following number in the sequence will be $7$ more than the previous number" then you will have given us an unambiguous way to continue the sequence and now we would have enough information to prove the claim. You have not told us this however and so there is nothing stopping the sequence to have continued $3,10,17,24,31,1,1,1,1,1,1,1,1,1,42,1,1,1,\dots$ – JMoravitz Sep 12 '20 at 16:47
  • 1
    I assume OP meant we are taliking about an arithmetic sequence where $a_1 = 3$ and $d=7$. Now he wants to prove this sequence is equivalent to his formula of $7n -4$ – dvd280 Sep 12 '20 at 16:52
  • 2
    And although that is a safe assumption, it is still a huge assumption and the OP needs to understand the ambiguity and impossibility of their question as currently written. Being forced to assume things and making incorrect assumptions lead to incorrect answers. http://spikedmath.com/492.html – JMoravitz Sep 12 '20 at 16:53
  • 3
    @JMoravitz my sincerely apologies I indeed didn't told you that each number in the sequence increases with +7. I've added it now in the question. – superkytoz Sep 12 '20 at 17:24
  • @superkytoz I took the liberty and moved it closer to the problem definition, not to be confused with the conclusion. – Sil Sep 12 '20 at 17:34
  • @dvd280 That is correct! – superkytoz Sep 12 '20 at 20:45
  • @JMoravitz I have edited the question to make it more specific. It's more specific now because I have given more clarity about where I'm exactly stuck at. Can you or someone else maybe help me now? Thanks in advance again. – superkytoz Sep 17 '20 at 20:25
  • How to write a clear induction proof, I need help with proofs using mathematical induction: $2+7+12+17+…+(5n-3)=(\frac{n}{2})(5n-1)$. Search elsewhere around this site as well for key phrases like "induction" and "arithmetic series" and similar to find dozens if not thousands more questions that should be useful to you. – JMoravitz Sep 17 '20 at 20:29

2 Answers2

0

The induction step will be trivial.

Assuming the $k$th term is given by $7k+4$, the $(k+1)$th term is $(7k+4) + 7 = 7(k+1)+4$.

This completes the induction.

player3236
  • 16,413
  • 2
    How do you know that the $k+1$'st term is necessarily going to be $7$ more than the previous term? That pattern can only be confirmed with what was written for the first few entries in the sequence but doesn't necessarily need to be true for later entries in the sequence. – JMoravitz Sep 12 '20 at 16:50
  • I do not. However do note that if, in primary school, if you are asked the next term for $2,4,6,8$ and your answer is $34$ because $T_n = 2n+(n-1)(n-2)(n-3)(n-4)$, you will be right but still be wrong. Sometimes simplicity is key; and I'll gladly take the downvote. – player3236 Sep 12 '20 at 17:00
-1

Let $a_n$ be the $n$'th term in an arithmetic sequence, where:

$$ a_1 = 3 $$ $$ d = 7 $$ We find the $n+1$ term as: $$ a_{n+1} = 3 + 7n $$ If the the sequence is arithmetic, then : $$ a_{n} = a_{n+1} - 7 $$ $$ \downarrow $$ $$ a_{n}+7 = a_{n+1} $$ Now we can see from the third row and the last row: $$ a_{n+1}= a_n + 7 $$ $$ a_{n+1} = 3 + 7n $$ $$ \downarrow $$ $$ a_n + 7 = 3 + 7n $$ $$ a_n = 7n-4 $$

dvd280
  • 676