3

When we talk about a straight line :

$$ y=mx+b $$

a line is parallel to another if their $m$ is the same (disregarding the $b$), is that right?

What happens when we talk about a curve such as:

$$ y=nx^2+mx+b $$

If we have two curves like this, how can we judge if they are parallel or approximately parallel?

EDIT:

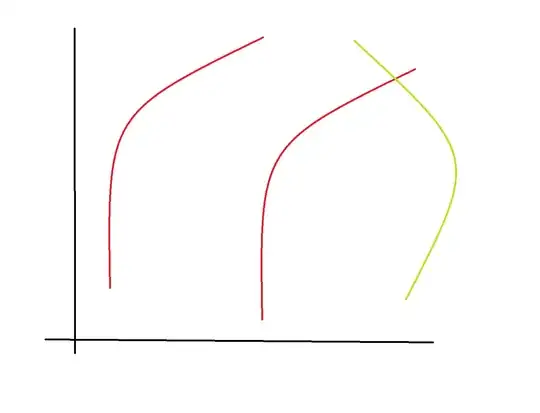
I'm sorry for the rough drawing enter image description here

but in the image you can see two red curves (let's say they are generated by polynomials of degree 2) and one green curve. I would like some judgment that let me know that the red curves are ( even approximately ) parallels while the green one is not.

KansaiRobot
  • 273
  • 2
    There is no notion of "parallel curves", only two lines can be parallel. Maybe do you mean "disjoint curves", i.e. curves that don't intersect each other? – Crostul Sep 12 '20 at 00:08
  • 2
    See, for instance, Wikipedia's "Parallel curve" entry, which captures the notion of curves that are equidistant from each other along normals. (This may-or-may-not match your intention.) As noted in the entry, "Except in the case of a line or circle, the parallel curves have a more complicated mathematical structure than the progenitor curve." In particular, a parallel curves of the parabola $y=nx^2+mx+b$ will not themselves be parabolas. – Blue Sep 12 '20 at 00:30
  • How about two polynomials of degree 2, how can you judge they are "almost parallel"? – KansaiRobot Sep 12 '20 at 00:31

1 Answers1

2

Two curves are parallel if at any point you draw a line perpendicular to the tangent line and passes through the point of tangency (the normal line), the normal lines are all parallel, at any point along the curve, and the distance between the line's points of intersections with the two curves are all the same.

See here: Math Curve Parallel Curves

KingLogic
  • 1,441
  • Is there a way to check for it based on the equation of the curves? – KansaiRobot Sep 12 '20 at 00:13
  • @KansaiRobot See Crostul's comment above. What exactly do you mean by "parallel curves"? Do you mean that, for example, if a road is built between the two curves, it would have same width throughout? – KingLogic Sep 12 '20 at 00:17
  • Yes, basically that. I will edit my question to add this – KansaiRobot Sep 12 '20 at 00:25
  • @KansaiRobot With the information, you can use code to give you the parallel curve. I don't think there currently exists a formula to check the parallelism of curves. – KingLogic Sep 12 '20 at 00:40
  • Actually I have two curves already generated and their equations and I would like to establish a threshold to check how "parallel" they are – KansaiRobot Sep 12 '20 at 00:44
  • 1
    @KansaiRobot Can you include the equations of the two curves into the question? That'll make it easier for us to answer. – KingLogic Sep 12 '20 at 00:48