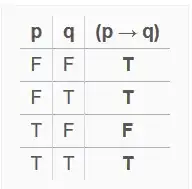
I have read this thread but it does not honestly answer why the implication truth table is defined the way above?
Suppose human kind has not yet made a logical system and you are the first one making one, why would you define the implication truth table the way above? I don't have problem with the way operations AND, OR are defined but with implication it is not clear.
What if the implication table was not defined the way above? Why we have rows like $p=F$ and $q=F$ but the implication is vacuously true?
In addition, are there any resources out there explaining how one would go about making a logical system? Is logical system that we use(here boolean logic) unique?
Asked
Active
Viewed 1,112 times
0
FreeMind
- 2,539
- 3
- 20
- 41
2 Answers
3
Intuitively, that is because an implication is false if and only if there exists a counterexample, i.e. a case where $p$ is true and $q$ false.
Formally, $p\to q\;$ is $\;\lnot p\vee q$, which corresponds to this truth table.
Bernard
- 175,478
-
What about the first line $\text{F} \rightarrow \text{F} = \text{T}$? If A implies B and A is false, you can't conclude that B is false? – Sep 12 '20 at 00:48
-
1@SenZen The first and second lines say: When given that $p$ is false, then $p\to q$ may be satisfied by $q$ being either true or false, therefore we cannot conclude anything about the truth of $q$ when given $p$ is false and $p\to q$ is true. Which is exactly the behavior we require. We do not want $p\to q$ to infer anything about $q$ when $p$ is false. We only require $p\to q$ to be a promise that $q$ will be true when $p$ is true. – Graham Kemp Sep 12 '20 at 01:08
-
We want "If $p$, then $q$" to be a promise that it is not so that $p$ is true and $q$ false. $~$ That is: $p\to q$ is equivalent to $\neg(p\wedge\neg q)$. $~$ Thus the only line where $p\to q~=\mathsf F$ is the third: where $p=\mathsf T$ and $q=\mathsf F$. – Graham Kemp Sep 12 '20 at 01:22
2
Consider this statement: "For all real numbers $x$, if $x < 4$ then $x < 6$."
Intuitively, this should be True -- do you agree?
So for example, when $x = 19$, we must have that the statement
"if $19 < 4$ then $19 < 6$" is True.
Ned
- 3,852
-
Do you agree that such answer only justifies what the truth table is rather than explaining why is it the way it is? To be more clear, why do we need if $19<4$ then $19<6$ to be a true statement? What if we consider it a false statement does it make any problem? – FreeMind Sep 12 '20 at 19:55
-
1We went the semantics of "For all $x$, $A(x)$" to be simply TRUE if and only if $A(x)$ holds for all values of $x$ -- we DON'T want a special case for $A(x)$ being an implication. To be brief, given that we want "If $x<4$ then $x<6$" to be true, we want that to mean it is True for ALL possible values of $x$, which includes $x=19$. – Ned Sep 12 '20 at 20:00
-
1@FreeMind If we just changed the truth table so that (FALSE implies FALSE) was assigned FALSE and left the rest of it alone, then the truth value of ($p$ implies $q$) would be identical to $q$ itself, so we wouldn't have any use for a connective defined that way. – Ned Sep 12 '20 at 22:27