The sphere minimises Willmore energy for genus $0$; the stereographic projection of the Clifford torus – major radius $1$, minor radius $1/\sqrt2$ – does so for genus $1$. While corresponding minimisers for higher genera have not been proven, there are already some good guesses. This page says (in French):
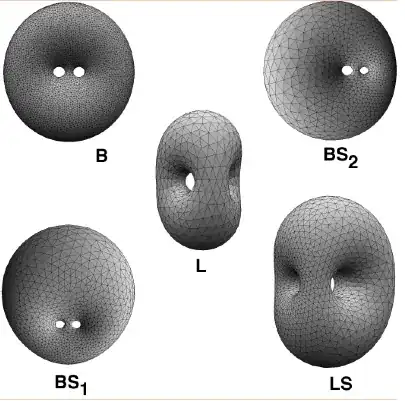
Blaine Lawson and Rob Kusner predicted that the analogue of the Clifford torus for genus $2$ is the following "button" and all its conformal transformations [Willmore energy is preserved under such transformations]:
Just as I rendered the Clifford torus for genus $1$ in Blender – see this other question of mine – I now want to render this genus-$2$ surface, particularly the one marked L which is most symmetric. The problem is that I have no idea how to do so with the given equations.
The relevant paper is R. Kusner, Comparison surfaces for the Willmore problem, Pacific J. Math. 138, no. 2 (1989), 317–345. The construction of the surface above – as well as other Willmore energy minimisers for higher genera – is described as follows:
Fix integers $m,k\ge0$ and let $$A_p=(e^{ip\pi/(k+1)},0),B_q=(0,e^{iq\pi/(m+1)})$$ in $\mathbb S^3$ (which we regard as the unit sphere in $\mathbb C^2=\mathbb R^4$). These are the endpoints of a (unique) shortest geodesic arc $A_pB_q$ in $\mathbb S^3$. The geodesic polygon $$\Gamma_{m,k}=A_0B_0\cup B_0A_1\cup A_1B_1\cup B_1A_0$$ bounds an area minimising disc $\delta_{m,k}\subset\mathbb S^3$. Repeated reflection of $\delta_{m,k}$ around the geodesics $\{A_pB_q|0\le p\le k,0\le q\le m\}$ produces [Lawson's] compact surface $\xi_{m,k}$. …
Recall from section 3 the compact minimal surface $\xi_{g,1}\subset\mathbb S^3$. Let $M_g\subset\mathbb R^3$ denote its compact stereographic image. Clearly $M_1$ is a standard torus and in fact, $[M_g]=g\mathbb S$ [which means that $M_g$ is topologically equivlent to the sum of $g$ tori]. By Fact 1.5 and Proposition 3.2 we deduce immediately $$W_O=4\pi\text{ and }W_{g\mathbb S}\le W(M_g)=\operatorname{area}(\xi_{g,1})<8\pi.$$ [$W_x$ means the minimal Willmore energy attained by surfaces topologically equivalent to $x$.]
In brief, what I want to do is to represent Lawson's $\xi_{2,1}$ surface in $\mathbb S^3$. After I do this, I can stereographic-project this down to $\mathbb R^3$, obtaining $M_2$ which should look like surface L in the image above after a rotation. I should be able to render $M_3,M_4,\dots$ surfaces analogously.
How can I get an exact representation of $\xi_{2,1}$, using the description above, as an explicit set of equations that will generate all points on the surface?
2023 edit: Lawson's original paper clarifies some things. In four dimensions $\xi_{m,k}$'s fundamental domain's boundary comprises four geodesic arcs connecting $\left(\cos\frac\pi{2(m+1)},\pm\sin\frac\pi{2(m+1)},0,0\right)$ and $\left(0,0,\pm\sin\frac\pi{2(k+1)},\cos\frac\pi{2(k+1)}\right)$. The arcs become circles passing through antipodes of the unit $2$-sphere upon stereographic projection to three dimensions, and by symmetry we only need a quarter of the domain. Surface Evolver with a custom surface energy integrand $(1+r^2)^{-2}$ (so that the integral gives the four-dimensional area up to a constant) followed by postprocessing transformations finally allowed me to render accurate $\xi_{m,k}$ surfaces for arbitrary $m,k$:





I still have no idea of how to get an exact parametrisation though. I can derive the formula for mean curvature of a surface embedded in the $3$-sphere in terms of the 3D parametric equations (involving a ternary 4D cross product), but it is far too complicated to be useful.