If a real number can be expressed in terms of complex solutions of cubic equations, can it be expressed in terms of real solutions of cubic equations?

Question

The motivation for this is to generalize the constructible numbers to higher degrees than $2$. Complex square roots can be expressed in terms of real square roots.

Suppose we have an algebraic number $\alpha\in\mathbb R$, which is contained in a tower of fields (excuse the notation; these are not finite fields):

$$\alpha\in\mathbb F_m\supset\mathbb F_{m-1}\supset\cdots\supset\mathbb F_1\supset\mathbb F_0=\mathbb Q,$$

where all $m$ extensions $\mathbb F_{k+1}/\mathbb F_k$ have degree $3$ or $2$. This means each element of $\mathbb F_{k+1}$ can be expressed using addition, subtraction, multiplication, division, elements of $\mathbb F_k$, and a single element not in $\mathbb F_k$ which solves a cubic equation with coefficients in $\mathbb F_k$. (Anything solving a quadratic equation $x^2+ax+b=0$ also solves a cubic equation $x^3+ax^2+bx=0$.)

These are sub-fields of $\mathbb C$. Must there be such a tower of sub-fields of $\mathbb R$?

---

One possibility is to simply take $\mathbb G_k=\mathbb F_k\cap\mathbb R$, so that

$$\alpha\in\mathbb G_m\supseteq\mathbb G_{m-1}\supseteq\cdots\supseteq\mathbb G_1\supseteq\mathbb G_0=\mathbb Q;$$

then we only need to show that each extension has degree $\leq3$ (or can be expanded into a sub-tower with degrees $\leq3$). Clearly if $\mathbb F_k\subset\mathbb R$, then $\mathbb G_k=\mathbb F_k$ and $[\mathbb G_{k+1}:\mathbb G_k]\leq[\mathbb F_{k+1}:\mathbb G_{k+1}][\mathbb G_{k+1}:\mathbb G_k]=[\mathbb F_{k+1}:\mathbb F_k]\leq3$. So we need to consider the extensions $\mathbb G_{k+1}/\mathbb G_k$ where $\mathbb F_k\not\subset\mathbb R$.

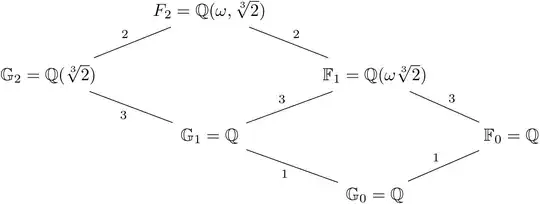
Here's an illustration of an example, with $\omega=\frac{-1+\sqrt{-3}}2\not\in\mathbb R$ and $\alpha=\sqrt[3]2\in\mathbb R$:

The diagonal lines denote extensions. Notice that $[\mathbb G_2:\mathbb G_1]=3\not\leq2=[\mathbb F_2:\mathbb F_1]$.

---

Any real solution of a real cubic equation can be expressed using complex cube roots (and square roots). In the irreducible case, the solutions cannot be expressed using real cube roots. These solutions are allowed here; I'm not requiring radical extensions.

If $\alpha$ is quartic over $\mathbb Q$, then it can be expressed using real solutions of cubic equations, as shown here.

Answer 1

For the constructible numbers, any quadratic extension is a radical extension, and there must be a first non-real field, which is gotten by adjoining $\sqrt a$ for some real $a<0$; then we can just write $\sqrt a=i\sqrt{|a|}$. Thus, after repeatedly applying the formula for complex square roots, performing the required complex arithmetic, and finally discarding the $i$ component, any constructible $\alpha\in\mathbb R$ can be written in terms of real square roots.

Similarly, for the cubic-constructible numbers, there must be a first non-real field, which is gotten by adjoining $\beta=\omega\sqrt[3]{a+\sqrt b\,}+\omega^2\sqrt[3]{a-\sqrt b\,}$ where $b>0$. This has the form $c+di$ where $c$ and $d$ are real-cubic-constructible:

$$\beta=\frac{-1+i\sqrt3}{2}\sqrt[3]{a+\sqrt b\,}+\frac{-1-i\sqrt3}{2}\sqrt[3]{a-\sqrt b\,}$$

$$=-\frac12\left(\sqrt[3]{a+\sqrt b\,}+\sqrt[3]{a-\sqrt b\,}\right)+\frac{\sqrt3}{2}\left(\sqrt[3]{a+\sqrt b\,}-\sqrt[3]{a-\sqrt b\,}\right)i.$$

Clearly, complex numbers of this form are closed under field operations. They're also closed under cube roots:

$$(x+yi)^3=a+bi$$

$$x^3-3xy^2=a,\quad3x^2y-y^3=b$$

$$3xy^2=x^3-a,\quad(3x^2-y^2)y=b$$

$$\big(9x^3-(x^3-a)\big)y=3bx$$

$$(8x^3+a)^2y^2=9b^2x^2$$

$$(8x^3+a)^2(x^3-a)-27b^2x^3=0.$$

This equation is $9$th degree in $x$, but it's $3$rd degree in $x^3$; furthermore, evaluating at $x^3\to-\infty,\;x^3=-a/8,\;x^3=a,\;x^3\to+\infty$ shows three sign changes, so we can solve for three different values of $x^3$. Taking a real cube root gives $x$, and the middle equation gives $y$ in terms of $x$. So we get three cube roots of $a+bi$. (This applies to the general case $ab\neq0$, but the special cases are easy to handle.)

This shows that the real part of anything expressible with complex square and cube roots is expressible with real solutions of cubics.

---

This approach probably doesn't generalize to degrees higher than $3$ or $4$.