I wrote a program to investigate how quickly $\sin{x}$ converges by seeing how long it took for an $x$ to differ from a partial sum by a certain amount. Here's a graph for the $n$th partial term with $n$ on the $x$-axis and the first $x$ to significantly differ (by more than 0.01) on the $y$-axis.
It looks very linear which I found surprising and interesting. I'd appreciate if someone had a proof or heuristic as to why this is the case.
Consider that $$\sin(x)=\sum_{n=0}^p\frac{(-1)^n}{(2 n+1)!} x^{2 n+1}+\sum_{n=p+1}^\infty\frac{(-1)^n}{(2 n+1)!} x^{2 n+1}$$ and, since it is an alternating series, you want to know what is $p$ such that $$\frac{x^{2p+3}}{(2p+3)!} \leq \epsilon \implies (2p+3)! \geq \frac{x^{2p+3} } \epsilon$$ This is almost exactly what I asked in this question. Adapted to your problem and this formulation, this should give $$2p+3 \sim e x \exp\Big[W(t) \Big]-\frac 12 \qquad \text{where} \qquad t=-\frac{\log \left(2 \pi x \epsilon ^2\right)}{2 e x}$$ $W(t)$ being Lambert function. So $$p\sim \frac{e}{2} x e^{W(t)}-\frac{7}{4}$$ and, for sure, you will use $\lceil p\rceil$.
Now, the problem is that $t$ will be very large (for example $x=\frac \pi 2$ and $\epsilon=10^{-20}$ would give $t=10.5172$). But we can use the expansion given in the Wikipedia page $$W(t)=L_1-L_2+\frac{L_2}{L_1}+\frac{(L_2-2) L_2}{2 L_1^2}+\frac{(2 L_2^2-9L_2+6) L_2}{6 L_1^3}+ ...$$ where $L_1=\log(t)$ and $L_2=\log(L_1)$.
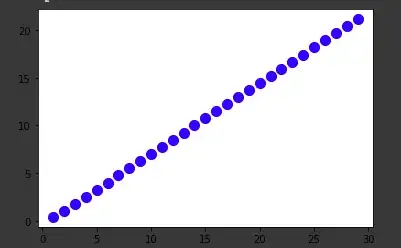
But, if $t$ is small, the result is "quite close" to linearity (as you observed).
This is what happens near zero since $\lim\limits _{x\to0}\frac{sin x}{x}$=1 . But when x is large, this is not true since the limit will be zero as x goes to infinity.
