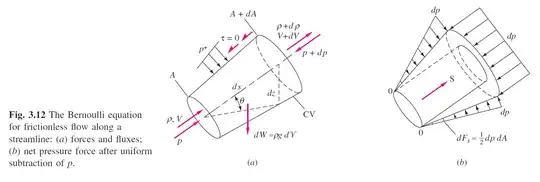
The net force in the $x$-direction due to pressure (in excess of the reference pressure $p$) acting on the circular cross-section on the extreme right is clearly $-dp \,(A +dA)$ -- the product of the excess pressure $dp$, assumed constant here, times the cross-sectional area $A + dA$.
If $\theta $ is the angle between the lateral surface and the $x$-axis, then the lateral surface area is $dA/\sin \theta$. The excess pressure can be assumed to vary linearly in this approximation for small $dA$ from $0$ on the extreme left to $dp$ on the extreme right. The average excess pressure is then $dp/2$ and the net force in the $x$-direction is given by
$$dF_{x, \,\text{side}}= \frac{1}{2} \ dp \cdot \frac{dA}{\sin \theta} \cdot \sin \theta = \frac{1}{2} \ dp \ dA,$$
where the last multiplication by $\sin \theta $ is used to obtain the component of the lateral force in the $x$-direction.
Adding together we get
$$dF_x = \frac{1}{2} \ dp \ dA- dp\,(A + dA) = -A \,dp - \frac{1}{2} \, dp \, dA$$
Assuming that the second term on the RHS is negligible with respect to the first term, since it involves a product of small quantities $dp \cdot dA$, we get $dF_x \approx - A \, dp$.