I came across this post from 2016 and am curious about something one of the answers called "opaque". Unfortunately, that member appears to be inactive.
Measuring $\pi$ with alternate distance metrics (p-norm).
The question is about computing $\pi$ for $l_p$ spaces. Heres the part of Zach's answer I'm interested in:
The p=2 is the only p-norm that has the SO(3) Lie Group structure. In other words, it is rotation invariant. Try it, you can rotate the coordinate system without changing the length. You can't do that with the Taxicab metric, the length you get will change.
The deep answer to your question is that only p=2 has a continuous symmetry, rotation. All the other p-norms have a either a finite number of symmetries or symmetries. Here's the thing, a p-unit circle is something like every possible vector that can generated from the group glued together. Imagine starting with a small vector then copying and rotating it just a bit, attaching it to the original vector, then repeating with the copy. Eventually, you'll generate the circle. You generate any of the p-norm circles using a similar process using their symmetry, albeit a bit more opaque. So why is p=2 special? The circle is made with the shortest vectors, and only the shortest vectors available to construct it. Why? Because they're all the same length! This isn't true unless you're rotationally invariant and guess what? Only p=2 is!!
I thought about this before and figured there was nothing. Don't all $l_p$ circles (for $1\le p<2$ or $p>2$), have the symmetry of a square? So, I see how we could generate circles for $p=1,2,\infty$, but no more.
$p=1,\infty$ seem ambiguous to me, so I'm not particular how they work out. For $p=2$, Zach appears to be saying something like $\int_\gamma x|dx|\approx \gamma$ where $\gamma$ is an positive arc of the unit circle starting at $(1,0)$ and $\approx$ means homothetic. At least, if you rotate a vector repeatedly by a small positive amount then add all the resultants together in a path, you will have a circular envelope.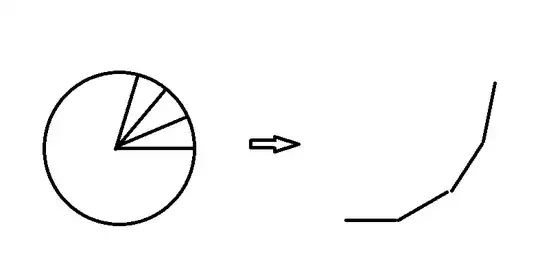
$l_2$ circle from the symmetry of the $l_2$ circle" />
To answer the question, you would need to provide a generalization of this aspect of $l_2$ to all values of $p$ for $1<p<2$.
