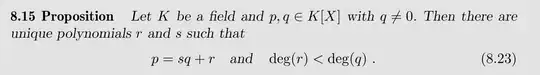I found that my 2 textbooks and other answers state this theorem for commutative ring:
- From textbook Algebra by Saunders MacLane and Garrett Birkhoff.
- From textbook Analysis 1 by Herbert Amann and Joachim Escher.
- In this answer, @Bill Dubuque also states for commutative ring.
For polynomials over any commutative coefficient ring, the high-school polynomial long division algorithm works to divide with remainder by any monic polynomial...
- In this answer, @Bill Dubuque also states for commutative ring.
Yes, your intuition correct: the Polynomial Factor Theorem works over any commutative ring since we can always divide (with remainder) by a polynomial that is monic i.e. lead coef $=1$ (or any unit = invertible element). Ditto for the equivalent Polynomial Remainder Theorem - see below.
I have re-read the proofs in my 2 textbooks and can not found where the commutativity is used. As such, is commutativity needed in the proof of division algorithm?