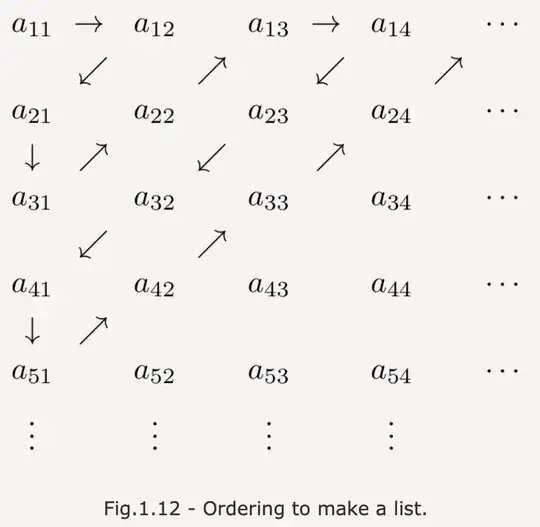
Does anyone know the reasoning behind the diagonal ordering in the second picture? I have seen it before, but am not sure what it's showing relating to this proof.
-
You can't prove this in ZF. You need something like axiom of choice for this to hold. – Jakobian Aug 29 '20 at 16:53
-
$AC$ or weaker $AC_\omega$ seems to be hidden in the choices of enumeration of the sets: $A_i={a_{i1},a_{i2},a_{i3},\ldots}$ (i.e. for every $i$ we choose one particular enumeration out of all enumerations available), rather than in the "diagonal" construction that follows. See also: https://math.stackexchange.com/a/2966801/700480 – Aug 29 '20 at 17:35
-
Yes you need AC for the theorem because you need to choose enumerations of all the $A_i$ to build the matrix. The zig-zag enumeration of the matrix is definable without AC. – Ned Aug 29 '20 at 17:35
-
I'm confused why the diagonal construction was used to "make a list that contains all the above lists". What property does this diagonal construction have that it is used in the proof? – Nick Aug 29 '20 at 18:19
-
@Nick It collects every element of every list exactly once, in effect turning the union of all those lists into one big list. Any other construction that would do the same would be just as good. Will edit my answer to say that. – Aug 29 '20 at 21:26
1 Answers
Do you need any reason further than just "it does the job!"? (It collects every element of every list exactly once, in effect turning the union of all those lists into one big list. Any other construction that would do the same would be just as good.)
I think that this example shows where our finite set intuition breaks when you switch to infinite sets.
If there were $n$ sets with $n$ elements each (with $n$ finite), you could use the same procedure, but much more likely you would go row-by-row or column-by-column.
Here you cannot do either because you can never enumerate the first row and switch to the second one (let alone third, fourth etc. - and similar for columns) so, somehow enumerating rows and columns "at the same time" is the only thing that can work.