10

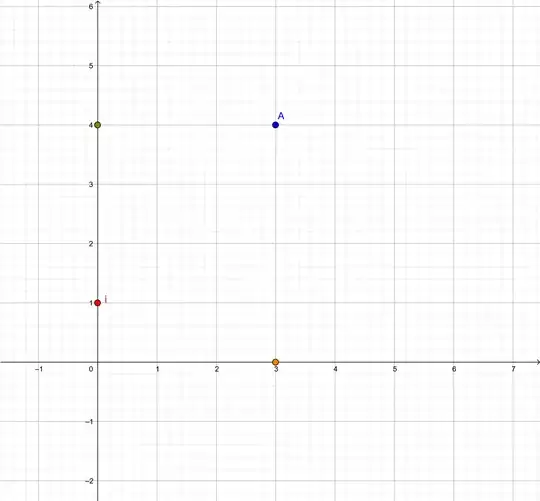
Mathematics could be defined as the study of formally defined abstractions. These abstractions may or may not be useful for describing real world phenomenon. Indeed, Physics could be defined as the subset of Maths that does describe real world phenomenon.

The integers - along with the operations of addition/multiplication - are incredibly versatile, and children can intuitively know when this abstraction is appropriate:

3 oranges

The Real Numbers, Sets, Vectors and even more complicated mathematical structures have obvious and intuitive real world correspondences.

From my experience with talking to people about "imaginary numbers", confusion is caused more often than not by the word "imaginary" and its difficult philosophical implications. If only I could explain that they are just as "real" as all the other abstractions they use every day!

So to aid in explaining the view that complex numbers and their associated operations are simply another useful abstraction that can be applied in the same way as the more familiar types of number:

What are some easy to grasp real world situations that can be elegantly abstracted and represented by complex numbers?

Update

I can see how this question is similar to this but it is subtly and crucially different. This question asks for simple real world situations. That question asks for simple applications and has received a bunch of answers about how complex numbers elagently deal with other mathematical abstractions. The top answers are all referring to simple areas of mathematics where complex numbers can be applied.

Community
  • 1
George Powell
  • 201
  • 2
  • 6
  • Wikipedia has a list. – vadim123 May 03 '13 at 13:16
  • Physics is not a subset of Math. Indeed, Math had a long struggle to get independent of Physics but initial ideas came from agricultural business, commerce, physics problems, etc... ( Counting, in general ). In Physics, we can think that Math is a way ( 'the way' ) to express ideas about the physical world albeit it is not always ( unfortunately ) possible. Your question is, indeed, quite interesting. – Felix Marin Feb 14 '14 at 23:59
  • Mathematics was physics (pythagoreans, geometry etc..). It was indeed physics expressed in symbolic form. The split into mathematics (esp.pure, not applied) and physics is a more recent one. Nevertheless, even pure math relate to (real) applications else they do not get studied or have any meaning. As i stated elsewhere "a Group is a Grup is a Group", and a Group is sth indeed connected and realizable in physical terms – Nikos M. Jun 01 '14 at 14:28
  • I agree this question is different. – Melvin Roest Dec 04 '19 at 17:52

4 Answers4

2

Actually a plethora of engineering domains use complex numbers (in circuits, mechanics, oscillations etc..) for example phasors

The reason this is done is because complex numbers by De Moivre's theorem relate nicely to periodic signals and systems, and treated using operations of multiplication/addition etc..

Also many trigonometric formulas are simplified if expressed in complex form (related to what is stated before).

These are indeed examples of real-world applications of complex numbers.

UPDATE: Another example of real-life complex arithmetic is clock-like arithmetic (sth similar to modulo arithmetic for integers). Meaning numbers of the form $e^{ia}$ where a is a real number. These numbers consitute a group ($U(1)$) the unitary group of 1 parameter and is also a Lie group. One can think of it as a counterpart of $\mathbb{Z_p}$ modular group but with real numbers.

NOTE A realist/constructivist approach to mathematcal entities need not be constrained in natural numbers only. Given interpretations (e.g as a process) indeed realist representations of these entities are not only possible but realizable as well.

Nikos M.
  • 2,158
  • +1 -- The linked page for "phasor" is sufficiently complex that it might make many people's eyes glaze over. It might thus be nice to offer a simple real-world example: if a circuit consisting of resistors, capacitors, and inductors is driven with a signal composed of sine waves at one or more frequencies, one can determine the behavior of the circuit at each frequency by regarding inductors and capacitors as though they have "imaginary" resistance, and then applying Ohm's law the same way as one would if the network contained only resistors. If the input contains multiple frequencies... – supercat Sep 13 '14 at 17:05
  • ...one can solve for each frequency independently, process the complex values back into sine waves, and add them together to describe the circuit's behavior with the actual driving waveform. Trying to model the behavior of a network containing many resistors, capacitors, and inductors would be difficult without complex numbers, but with complex numbers the behavior can be computed using straightforward arithmetic. – supercat Sep 13 '14 at 17:09
  • @supercat, yes exactly (for linear circuits, or analysis in the liner response region). Well phasors are simply 2-dimensional vectors that change with frequency (and can be added/multiplied like numbers, i.e complex numbers). So they make linear analysis a simple algebraic manipulation. But i think the main point is the capability to represent (and model) (realistic) periodic signals or processes (per the question). Like adding or subtracting or combining "rotations". This is a highly realistic/physical process modeled with complex arithmetic – Nikos M. Sep 13 '14 at 19:00
  • 1
    My point was that someone who isn't familiar with the use of complex math in describing circuits or similar phenomena is far less likely to understand talk of "phasors" than to understand "If inductors and capacitors are regarded as resistors with imaginary values, then techniques which would normally only be able to analyze combinations of resistors will be applicable to any combination of resistors, capacitors, and inductors." I don't know who first realized that Ohm's Law applies to RLC circuits, but I find it amazingly elegant. – supercat Sep 13 '14 at 20:43
  • @supercat, yeap maybe you have a point there, that is why i linked the wikipedia page (and hinted at general periodic/rotations modelling). Did not want to clutter the answer too much, if you have a suggection i can edit it though – Nikos M. Sep 13 '14 at 21:03
1

It is unlikely that genuinely "real world" examples can be found outside of the well known scientific and engineering applications. Such a real world situation would require a collection of "rotation" operations that can be combined in two different ways: composition (complex number multiplication) and addition.

Circular or periodic phenomena that admit rotations can be found in natural real-life examples, but having any addition operation at all (distinct from performing one rotation after another) is rare enough that it is hard to come up with examples. Having the two operations not only exist but obey the distributive law is very restrictive and seems to happen only in highly structured and mathematized situations whose abstract representation can be reformulated using complex numbers.

zyx
  • 35,436
0

Celestial mechanics!

Using a complex number $U$ as the basic variable, the equations of motion for a Keplerian orbit are

$$2\,\frac{d^2U}{ds^2}-E\,U=0$$

$$2\,\left|\frac{dU}{ds}\right|^2-E\,|U|^2=GM$$

$$\frac{dt}{ds}=|U|^2$$

where $E$ is the (constant) energy, $G$ is the gravitational constant, $M$ is the attractor's mass, and $t$ is time.

The position of the body in orbit is $U^2$. (In geometric algebra, this would be $U^2e_1=Ue_1U^\dagger$.)

Respectively, if $E<0,\,E=0,\,E>0$, then the solution to the first equation is an ellipse, straight line, hyperbola; and $U^2$ is an ellipse, parabola, hyperbola.

Source: http://geocalc.clas.asu.edu/pdf/SPINORPM.pdf

mr_e_man
  • 5,364
0

Complex numbers are not very abstract: in fact, everyone knows them, but under another name: points in a grid. The question reflects a misunderstanding of what a complex number is.

At the very beginning of the study of geometry, one learns to place points in a Cartesian frame, often an orthonormal frame.

The set of real numbers (or real line) is denoted $\mathbb{R}$; there is no distinction to be made between points $(x,y)$ of the euclidean plane $\mathbb{R}\times\mathbb{R}$ and complex numbers $x+iy$; if we note $\mathbb{C}$ the set of complex numbers instead of $\mathbb{R}\times\mathbb{R} $ or $\mathbb{R}^2$, it is just to remember that in addition to the addition of the vectors in $\mathbb{R}\times\mathbb{R} $, there is defined a multiplication which makes $\mathbb{C}$ a field.

For a nod to the image with the three oranges, here is an illustration of the complex number $\color{blue}A=\color{orange}3+\color{green}4i$ : enter image description here

Stéphane Jaouen
  • 2,954
  • 5
  • 21