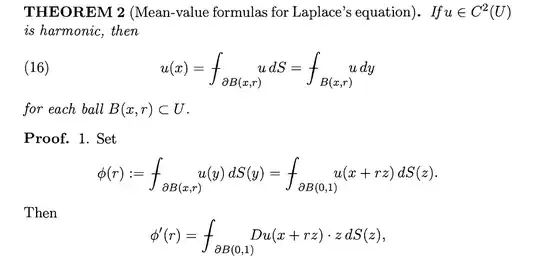1

enter image description here

For the integral $⨍_{\partial B(0,1)}u(x+rz)dS(z),$ shall we interpret it as $\frac{1}{m(\partial B(x,r))}\int_{\partial B(0,1)} u(x+rz)dS(z)$? I think there is some abuse of notation. Please correct me if I am wrong.

000000000
  • 497
  • Usually the bar means “divide by the measure of the integration domain”. Note that they are using change of variables here. The Jacobian is $r^{n-1}$ (cause you have to differentiate along the sphere, so you loose one power) which is how the measure of the $(n-1)$-sphere scales. – Sven Pistre Aug 25 '20 at 08:22
  • What I wanted to convey is that indeed $\frac{1}{m(\partial B(x,r))} \int_{\partial B(x,r)} u(y)dS(y)=\frac{1}{m(\partial B(0,1))} \int_{\partial B(0,1)} u(x+rz)dS(z)$! The point here is to get rid of the $r$-dependance of the integration domain and put all $r$’s into the integrand so that the derivative can be calculated more easily. – Sven Pistre Aug 25 '20 at 08:50
  • yes! I think I get your point. I am wondering how to show the equlity holds? – 000000000 Aug 25 '20 at 09:19
  • https://math.stackexchange.com/questions/673526/how-to-change-variables-in-a-surface-integral-without-parametrizing – 000000000 Aug 25 '20 at 09:33

1 Answers1

1

See page 702 in Evans for a definition. But you are right by definition

$$⨍_{\partial B(0,1)} u(x+rz) dS(z) = \frac{1}{m(\partial B(0,1))} \int_{\partial B(0,1)} u(x+rz)dS(z).$$

To see that $$⨍_{\partial B(x,r)} u(y) dS(y) = ⨍_{\partial B(0,1)} u(x+rz) dS(z)$$ use the notation in Evans and the hint from Sven Pistre. Note that $n\alpha(n)$ denotes the surface area of the $(n-1)$-dimensional unit sphere and that the Jacobi Determinant of the change of variables is $r^{n-1}$.

$$\begin{align*}⨍_{\partial B(x,r)} u(y) dS(y) &= \frac{1}{n\alpha(n)r^{n-1}} \int_{\partial B(x,r)} u(y) dS(y) \\\\ &= \frac{r^{n-1}}{n\alpha(n)r^{n-1}} \int_{\partial B(0,1)} u(x+rz)dS(z) \\\\ &=\frac{1}{n\alpha(n)} \int_{\partial B(0,1)} u(x+rz)dS(z) \\\\ &=⨍_{\partial B(0,1)} u(x+rz) dS(z),\end{align*}$$

where we used a change of variables $y = x+rz$ in the second equality.

Sven Pistre
  • 1,320
SC2020
  • 719