In the theory of finite loopy stopper combinatorial game values, which, in some sense, includes a copy of the ring of dyadic rationals (fractions with denominators that are a power of 2), there is a "smallest positive game value". It is denoted 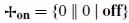 , although Conway also called it tiny.
, although Conway also called it tiny.
Without developing all of the formal theory, I'll try to describe the idea: Two players, Left and Right are playing a bunch of games together (on each turn, they choose one of the games to make a move in), alternating turns. If it's their turn to move but they have no legal move, they lose. Now, if tiny is one of the games, and it's Left's turn, she can move to end the tiny game (so that component has no more legal moves for anyone), and Right doesn't have this luxury, so tiny confers some advantage to Left (measured by the game value). However, if it's Right's turn to move and tiny is available, he can make a move that Left essentially must respond to immediately (because if she doesn't, Right will gain the ability to "pass" and never run out of moves). This would be the biggest possible threat against Left, which makes tiny the smallest possible advantage for Left.
Now, it's really important to note that the extent to which these games act like numbers is extremely limited, although some games are just like numbers we know (1/2, 3, -4+1/8, etc.), and everyone else's comments to the effect of "this doesn't make sense when dealing with numbers" are absolutely valid. Even in the Surreal Numbers (which, in some sense, include everything that you'd want to call a "positive number", in any context), there is no such thing as a smallest positive number.
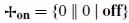 , although Conway also called it tiny.
, although Conway also called it tiny.