3

In this video lecture on tensor calculus, around 2:36 he takes gradient of a geometric "length function" which increases outwards in direction of length. But I don't understand direction the gradient should be in? does different points have different gradients ? And what exactly is the technicality for defining a function from three points?

I thought of constructing trying to describe what he did using coordinates as follows:

Take three points $ A_1,A_2,A_3$

Now, from these three fixed points we take a point in the triangle $ (x,y)$

Let $d(A_i(x,y))$ be distance of our point from the vertex A Our goal is to minimize:

$$ D(x,y) = \sum_{k=1}^{3} d(A_i (x,y) )$$

Supposedly we take the gradient of both sides and set the left to zero, we get,

$$ 0 = \nabla \sum_{k=1}^{3} d(A_i (x,y)) $$

or,

$$ 0 = \sum_{k=1}^{3} \nabla d(A_i (x,y) ) $$

And the point where the three unit vectors of $ d(A_i (x,y))$ go to zero is our Torricelli point, But I don't quite get how he define the functions based on distances from vertex. What exactly is the technicalities of this?

Further, I can't find a similar proof online, is this not a well documented proof?

Edit: On some more thought, could I use a similar method for finding the 'Torricelli point' of more complicated shapes? seems like it should easily be doable by the same principles.

For example, finding the 'toricelli point' of the pentagon reduces to the problem of finding a way to arrange the 5 unit vectors such that their sum is zero as shown below. Further speaking, how would one generally find an arrangement such that adds to zero? enter image description here

tryst with freedom
  • 11,538

1 Answers1

1

There are many questions. Let's try to make a list.

  1. "does different points have different gradients ?"

Yes, they do. The gradient of a function is a vector field, meaning the vector varies form point to point.

  1. "But I don't understand direction the gradient should be in?"

"I don't quite get how he define the functions based on distances from vertex. What exactly is the technicalities of this?"

Geometrically we have 2 properties of the gradient:

a) The gradient points in the direction of the fastest increase of the function.

For the function "distance to O" the direction of fastest increase at some P (as per answer to part 1, this will vary as P varies) is the direction of moving along the ray OP, "out from O". Again, this direction varies as we vary P.

b) The size of the gradient is the change in the function per step in the gradient's direction (in the limit of very small steps).

For "distance from O" what this is saying is that we should compute how much the "distance from O" changes as we take a step of size $\Delta$ along the ray OP. The answer is $\Delta$. The ratio of increase in function by the step size is 1. Hence the gradient vector is of length 1 (for any P).

Alternatively, you could write $f(P)=|OP|$ and take gradient. Let's assume O is point with (fixed) coordinates $(x_0, y_0)$ and $P$ has variable coordinates $(x, y)$.

To compute gradient of $f(P)=f(x,y)=|OP|=\sqrt{(x-x_0)^2+(y-y_0)^2}$ we use the fact that square distance is a nicer function than distance (being $f^2(P)=(x-x_0)^2+(y-y_0)^2)$, hence quadratic polynomial). So, we use the chain rule, $\nabla_P f^2(P)=2 f(P) \nabla_P f^2(P)$; and $\nabla_P f^2(P)=(2(x-x_0), 2(y-y_0))=2 OP$. Together this gives $\nabla_P f(P)=\frac{OP}{|OP|}$, aka the unit vector pointing out along the ray OP, same as we got from geometric reasoning above.

  1. "could I use a similar method for finding the 'Torricelli point' of more complicated shapes?"

Well, the part where the 'Torricelli point' is the one where unit vectors from the point to the vertices sum up to zero is indeed the same, and for the same reason. The problem is that for 3 vectors the only way this can be true is that the all have angles 120 between any pair of the vectors -- so that the Torricelli point must have this "120 degree" property. For any higher number of vectors, there are infinitely many possible configurations of unit vectors that sum up to zero. So the condition "the vectors sum to zero" is much less restrictive. It must be combined in some non-trivial way with the condition that these vectors point from P to the vertices of our polygon. It is not immediately clear to me how one would do this.

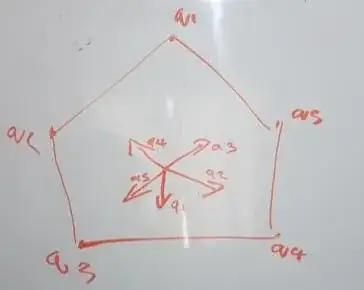
  1. "For example, finding the 'toricelli point' of the pentagon reduces to the problem of finding a way to arrange the 5 unit vectors such that their sum is zero as shown below. Further speaking, how would one generally find an arrangement such that adds to zero?"

Precisely. For 5 vectors you can easily produce many such arrangements: summing 2 unit vectors one can get a vector in arbitrary direction of any size between 0 and 2. Now take any triangle with one side $\vec{v}$ of size 1 and two others of sizes between 0 and 2. Make these two "other" sides by summing some pairs of unit vectors, and finally add the last unit vector equal to $\vec{v}$. The overall sum of 5 vectors is then the sum of the 3 vectors making up the triangle, i.e. $\vec{0}$.

Now, for a random configuration of this type you will not find a point P such that the vector from it to your 5 vertices make this configuration. Hence it is not clear how to find "Torricelli points" of pentagons using this kind of method.

Max
  • 14,233