I calculated $\cos(30^{\circ})$ and it is $\frac{\sqrt(3)}{2}$.
I calculated $\cos(-30^{\circ})$ and it is $\frac{\sqrt(3)}{2}$.
And, I don't know why? Can you explain me simply? I think that figures will be very much helpful.
I calculated $\cos(30^{\circ})$ and it is $\frac{\sqrt(3)}{2}$.
I calculated $\cos(-30^{\circ})$ and it is $\frac{\sqrt(3)}{2}$.
And, I don't know why? Can you explain me simply? I think that figures will be very much helpful.
This is because cosine is an even function, that is $\cos(-\theta)=\cos(\theta)$ (and also sine is an odd function so $\sin(-\theta)=-\sin(\theta))$.
Here is a sketch of the cosine function:
As the others said, the reason is because cos is an even function, but I just wanted to give you a nice insight into why cosine is even. So if you take the trigonometric definition of cosine $$\cos(\theta) = \frac{x}{r}$$, where $r$ is the distance from the origin to the point ($\sqrt{x^2+y^2}$), which is always positive despite the values of $x$ and $y$.
Now, in the first case, assume that $\theta$ is in the first quadrant ($\theta\in(0,\pi/2)$), then $-\theta$ will be in the fourth quadrant($\theta\in(\pi,\frac{3\cdot\pi}{2})$), but both in the fourth and first quadrant $x$ is positive, so $$\cos(\theta)=\frac{x}{r}=\cos(-\theta)$$ For more elaboration see the picture below.
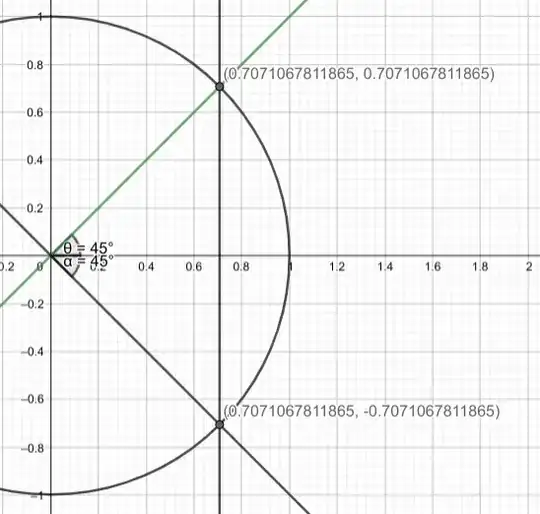
In the above picture as you can see $\alpha = -\theta$ but both of the angle corresponds to the same $x$ and opposite $y$. If you take one point as an example, you can see that both points correspond to $x = 0.707$ while for opposite $y's$, $0.707$ and $-0.707$. But as you know cos doesn't depend on the $y$ value. $$\implies \cos(\theta)=\cos(\alpha)=\cos(-\theta)= \frac{0.707}{\sqrt{0.707^2+0.707^2}}$$ This also works for the general case as long as $\theta$ is in the first quadrant.
Now, in the second case, assume that $\theta$ is in the second quadrant($\theta\in(\frac{\pi}{2},\pi)$), then $-\theta$ will be in the third quadrant($\theta\in(\pi,\frac{3\dot\pi}{2})$), but both in the second and third quadrant $x$ is negative so again $$\cos(\theta)=\frac{x}{r}=\cos(-\theta)$$ you can think of the above image reflected to get visualization.
You then don't have to think about the third and fourth quadrant because it is similar to proving it for the first and second quadrant. Therefore cosine is even which means $\cos(\theta) = \cos(-\theta)$ for any $\theta\in(0,2\cdot\pi)$
Draw a picture of a circle.
$\cos \theta, \sin \theta$ represent the $(x,y)$ values of a point on a unit circle at an angle $\theta$.
Isn't it clear and obvious that if you compare going clockwise around a circle versus going counter clockwise that the $x$ values will all be the same while the $y$ values will be opposite in sign? Just look at the picture:
So $\cos (-\theta) = \cos (\theta)=a$ and $\sin (-\theta) = -\sin \theta=-b$