I was using google graphs to find the graph of $$\frac{x^3-8}{x^2-4}$$ and it gave me:
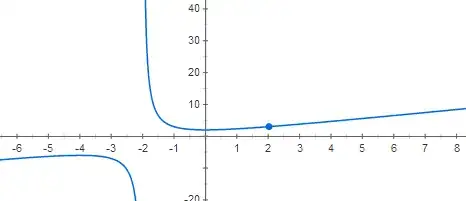
Why is $x=2$ defined as $3$? I know that it is supposed to tend to 3. But where is the asymptote???
I was using google graphs to find the graph of $$\frac{x^3-8}{x^2-4}$$ and it gave me:

Why is $x=2$ defined as $3$? I know that it is supposed to tend to 3. But where is the asymptote???
Because there is a removable singularity at $x = 2$, there will be no asymptote.
You're correct that the function is not defined at $x = 2$. Consider the point $(2, 3)$ to be a hole in the graph.
Note that in the numerator, $$(x-2)(x^2 + 2x + 4) = x^3 - 8,$$ and in the denominator $$(x-2)(x+ 2) = x^2 - 4$$
When we simplify by canceling (while recognizing $x\neq 2$), we end with the rational function $$\frac{x^2 + 2x + 4}{x+2}$$
We can confirm that the "hole" at $x = 2$ is a removable singularity by confirming that its limit exists: $$\lim_{x \to 2} \frac{x^2 + 2x + 4}{x+2} = 3$$
In contrast, however, we do see, that there is an asymptote at $x = -2$. We can know this without graphing by evaluating the limit of the function as $x$ approaches $-2$ from the left and from the right:
$$\lim_{x \to -2^-} \frac{x^2 + 2x + 4}{x+2} \to -\infty$$
$$\lim_{x \to -2^+} \frac{x^2 + 2x + 4}{x+2} \to +\infty$$
Hence, there exists a vertical asymptote at $x = -2$.
There is no asymptote at $x=2$. Note that $$\frac{x^3-8}{x^2-4}=\frac{(x-2)(x^2+2x+4)}{(x-2)(x+2)}.$$ For $x\ne 2$, we can cancel the $x-2$.
So near $x=2$ our function is very well behaved, it has a nice limit. The singularity at $2$ is called a removable singularity. If we define a new function $g(x)$ by $g(x)$ equal to our given expression when $x\ne 2$, and $g(2)= 3$, the function $g(x)$ is very nice everywhere except at $x=-2$. (The singularity at $x=-2$ is not removable.)
Many pieces of graphing software completely ignore removable singularities. At least Alpha had the decency to put a dot there.
There will only be an asymptote if the limit is infinity. in your case, for all points $x\neq 2$: $$\frac{x^3-8}{x^2-4} = \frac{x^2+2x+4}{x+2} $$ Which has no discontinuities!