1

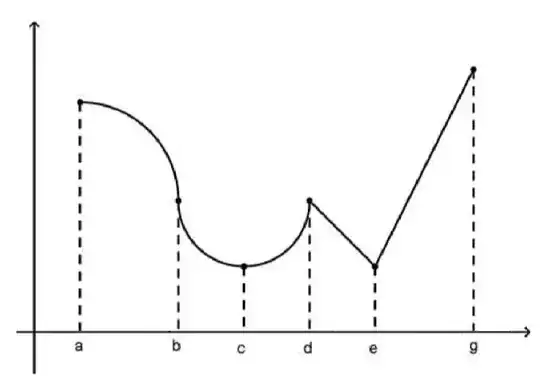
enter image description here

The reader is asked to identify the function's critical values. Point $x=c$ is a critical value because $f'(c)=0$. Also, points $x=b,d,e$ are critical values because $f'$ is undefined at those points.

Since critical values include points where $f'$ is undefined, would the endpoints $x=a$ and $x=g$ be included? If $f'(a)$ and $f'(g)$ are undefined, then they are considered critical values by definition.

According to this question and this question and this question, a function is still continuous at the endpoints of its domain, which would imply that

(1.) $$\lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x)$$

(2.) $$\lim_{x \to g^-} f(x) = \lim_{x \to g^+} f(x).$$

Continuity is a pre-requisite for differentiability, but not sufficient for differentiability, so we have to be careful. Would it also be correct that

(3.) $$\lim_{x \to a^-} \frac{f(x)-f(a)}{x-a} = \lim_{x \to a^+} \frac{f(x)-f(a)}{x-a}$$

(4.) $$\lim_{x \to g^-} \frac{f(x)-f(g)}{x-g} = \lim_{x \to g^+} \frac{f(x)-f(g)}{x-g}?$$

I don't see why it would be fair to say (1.) and (2.) are true but not (3.) and (4.).

If $f$ is not differentiable at $x=a$ and $x=g$, then these points should be called critical values, since the definition of critical values are points where $f'$ is zero or undefined. This would be advantageous! Careful students looking for local extrema will remember to check endpoints if they are technically considered critical values.

What is the official answer according to real analysis? Thanks for your thoughts!

EthanAlvaree
  • 3,412

1 Answers1

1

None of the claimed equalities are true because they simply do not make any sense. Limits are not defined by taking limits from the left and right sides. Rather, limits are based on taking limits from any direction within the domain. If the domain includes a left and right side of a point, then the limit is defined from the left and right sides. If there is only one side, then the limit is defined by that side. This is pointed out in the links you've provided.

In these cases, this is not the case, and we simply have

$$f(a)=\lim_{x\to a}f(x)=\lim_{x\to a^+}f(x)$$

$$f(g)=\lim_{x\to g}f(x)=\lim_{x\to g^-}f(x)$$

$$f'(a)=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}=\lim_{x\to a^+}\frac{f(x)-f(a)}{x-a}$$

$$f'(g)=\lim_{x\to g}\frac{f(x)-f(g)}{x-g}=\lim_{x\to g^-}\frac{f(x)-f(g)}{x-g}$$

whereas the limits from the opposite sides are nothing more than undefined.

It is worth noting that in more general settings, such as the complex numbers or $\mathbb R^2$, there is no notion of left or right sided limits, or perhaps the left and right sides are not the only sides to consider.

Simply Beautiful Art
  • 74,685
  • 1
    It's also worth noting that some authors only define the derivative at inner points of the domain. In that case, $f'(a)$ and $f'(g)$ would be undefined. The reason is that while limit points (like the interval boundaries here) are fine in one dimension, using them in higher dimensions would introduce problems. For instance, the derivative of a function defined on $\mathbb R\times{0}$ would not be unique. For this reason I personally prefer only defining a derivative at inner points of the domain. – Vercassivelaunos Aug 11 '20 at 05:22
  • @simply-beautiful-art It sounds like you are saying the endpoints are NOT critical values, since the derivative does exist at the endpoints, is that correct? – EthanAlvaree Aug 11 '20 at 05:28
  • @Vercassivelaunos Does this automatically make the endpoints critical values, since the derivative is undefined at those points? – EthanAlvaree Aug 11 '20 at 05:30
  • 1
    If you subscribe to the definition that derivatives require inner points, then yes. With @simply-beautiful-art's definition, no. You should check how your lecturer/textbook handles it. – Vercassivelaunos Aug 11 '20 at 05:42
  • Thank you for the thoughts. In my case, I am the lecturer, trying to decide which definition is standard. It seems to me only defining $f'$ for interior values is the optimal choice, since it ensures that endpoints would be critical values. Then I need only say "check critical values for local extrema", instead of saying "check critical values and endpoints for local extrema" (the latter would be redundant). – EthanAlvaree Aug 12 '20 at 06:12