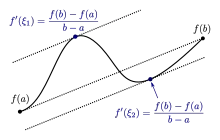The Generalized Mean-Value Theorem or Cauchy's theorem or of the finite increments theorem says:
If functions $f$ and $g$ are both continuous on $[a,b]\subset\Bbb R$ and differentiable on $]a,b[\subset\Bbb R$, and if $g'(x)\neq 0$ for every $x\in]a,b[$, then there exists a number $\xi$ in $]a,b[$ such that
$$\frac{f(b)-f(a)}{g(a)-g(b)}=\frac{f'(\xi)}{g'(\xi)}$$
If $g(x)=x$ I found the Lagrange's theorem.
This theorem says that it is also possible that there are multiple tangents parallel to the secant (see the image).
- What is the importance to have multiple tangents parallel to the secant in a specific exercise?
This theorem is now almost omitted from Italian school books: there is only the enunciate and few exercises.
I have taken an screenshot of a English book,
and I see many exercises of Lagrange's theorem to justify inequalities.
- At this point I ask to all users on Math.SE a curiosity: what could be good uses for the generalized mean-value theorem or of Cauchy?