Using the fact that $1+2+\cdots+n=\frac{n(n+1)}{2}$, we can deduce that sum of first $n$ positive odd integers is $n^2$. However, is there a way of finding the sum of $1+3+5+\cdots+(2n-1)$ visually?
Asked
Active
Viewed 171 times
1
-
6https://en.wikipedia.org/wiki/Proof_without_words#Sum_of_odd_numbers – Jaap Scherphuis Aug 10 '20 at 14:34
-
3https://www.youtube.com/watch?v=IJ0EQCkJCTc – abcd123 Aug 10 '20 at 14:39
-
4https://math.stackexchange.com/a/733805/179297 – JMoravitz Aug 10 '20 at 14:47
-
1$\displaystyle \begin{array}{ccc} \color{red}{\huge\bullet} & \color{magenta}{\huge\bullet} & \color{black}{\huge\bullet} \ \color{magenta}{\huge\bullet} & \color{magenta}{\huge\bullet} & \color{black}{\huge\bullet} \ \color{black}{\huge\bullet} & \color{black}{\huge\bullet} & \color{black}{\huge\bullet} \end{array} $ – Felix Marin Aug 11 '20 at 05:19
1 Answers
2
Here is a ‘proof’ I once found in a book for young children. It is not a real proof in the mathematical sense, but rather a convincing example that any mathematician feels could be transformed into a rigourous proof:
Imagine wooden cubes stacked in rows, with the basis containing, say, $7$ cubes, the row above, $5$ cubes, the row still above, $3$ and the last row $1$, like this:
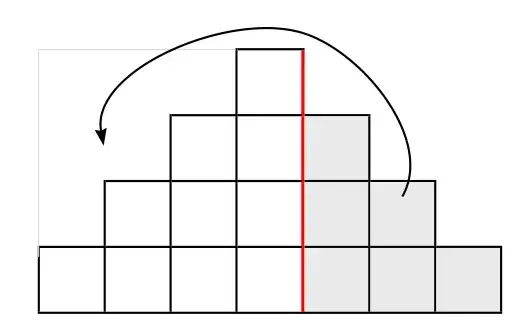
It is a geometrical evidence that, moving the grey squares from the bottom right corner to the top left corner, one recreates a square with sides equal to the number of rows, i.e. $4$ units, hence we have $16$ of them for the sum of the $4$ first odd numbers.
Bernard
- 175,478