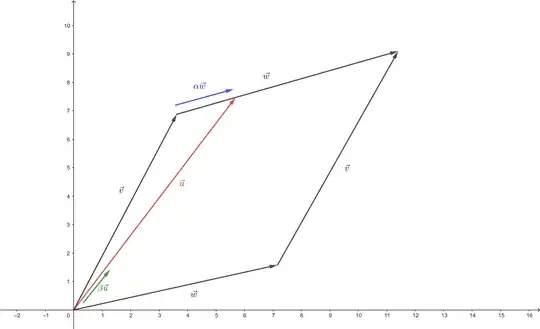
For vectors $\vec{v},\vec{w}\in\mathbb{R}^2$, prove that the combinations $c\vec{v}+d\vec{w}$ with $0 ≤ c ≤ 1$ and $0 ≤ d ≤ 1$ fill the parallelogram with sides $\vec{v}$ and $\vec{w}$
If I take a simple examples like $\vec{v}=(1,0)$ and $\vec{w}=(0,1)$ $$ c\begin{bmatrix} 1\\0 \end{bmatrix}+d\begin{bmatrix} 0\\1 \end{bmatrix}=\begin{bmatrix} c\\d \end{bmatrix}=\begin{bmatrix} x\in[0,1]\\y\in[0,1] \end{bmatrix} $$
But how do I prove it mathematically for the general case ?
This is stated by @Jack D'Aurizio in the post Decide if a point is inside parallelogram, but no proof is given.
My Attempt
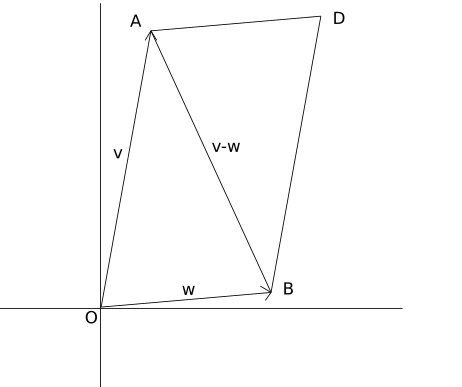 $$
\vec{r}=c\vec{v}+d\vec{w}\\
c,d\in[0,1]\implies c+d\in[0,2]\\
\text{when }c+d\in[0,1]\implies c\leq 1-d\\
\vec{r}\leq (1-d)\vec{v}+d\vec{w}=\vec{v}+d(\vec{w}-\vec{v}) \\
\implies\vec{r} \text{ fills the triangle }\Delta OAB\\
$$
When $c+d\in[1,2]$ how do I prove that $\vec{r}$ span the other half of the parallelogram ?
$$
\vec{r}=c\vec{v}+d\vec{w}\\
c,d\in[0,1]\implies c+d\in[0,2]\\
\text{when }c+d\in[0,1]\implies c\leq 1-d\\
\vec{r}\leq (1-d)\vec{v}+d\vec{w}=\vec{v}+d(\vec{w}-\vec{v}) \\
\implies\vec{r} \text{ fills the triangle }\Delta OAB\\
$$
When $c+d\in[1,2]$ how do I prove that $\vec{r}$ span the other half of the parallelogram ?