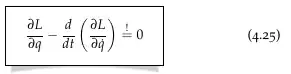Understanding the SI units of the Euler–Lagrange equation terms

Question

Page 88 of No-Nonsense Classical Mechanics states the Euler-Lagrange equation as follows:

Questions: I'm having trouble understanding just what the statement means.

Are $\frac{\partial L}{\partial q}$ and $\frac{\partial L}{\partial \dot{q}}$ directional derivatives?
What are the SI units of $\frac{\partial L}{\partial q}$, and won't they differ from $\frac{d}{dt} \left( \frac{\partial L}{\partial q} \right)$ due to the $\frac{d}{dt}$? If the units differ between these two terms, doesn't this equation "fail to make sense"?

The answer to (1) is that they are regular partial derivatives, you just need to understand what the notation means (which can be confusing at times), in particular what is the function, what the partial derivative symbols mean, where the derivatives are being evaluated etc. See this answer and also this answer (which addresses things in greater generality for when the Lagrangian is a function on the tangent bundle of the configuration manifold). If you need more elaboration let me know — peek-a-boo, Aug 09 '20 at 06:04

score 2 · Accepted Answer · answered Aug 09 '20 at 05:53

2

Let's suppose the units of $q$ are are $\text{u}$, which stands for "user units."

The units of $\frac{\partial L}{\partial q}$ are $\text{J}\text{u}^{-1}$ (Joules per user unit.)

The units of $\frac{\partial L}{\partial \dot q}$ are Joules per (user units per second) which is $\text{J}\text{u}^{-1}\text{s}$. Hence the units of $\frac{d}{dt}\left(\frac{\partial L}{\partial \dot q}\right)$ are $\text{J}\text{u}^{-1}$.

You could think of them as directional derivatives, but I think it is more helpful just to think of them as partial derivatives.

answered Aug 09 '20 at 05:53

Stephen Montgomery-Smith

26,430
2
35
64

How can they be thought of as partial derivatives? If our configuration space is in $\mathbb{R}^n$, do you mean to think of each them as a collection of $n$ partial derivatives (along each axis of $\mathbb{R}^n$)? – user1770201 Aug 09 '20 at 06:03
Yes. $\frac{\partial L}{\partial q}$ means $\left[\frac{\partial L}{\partial q_i}\right]_i$. – Stephen Montgomery-Smith Aug 09 '20 at 06:05
2

And the units of $q_i$ might be different from $q_j$. – Stephen Montgomery-Smith Aug 09 '20 at 06:06
Why might the units differ between $q_i$ and $q_j$? – user1770201 Aug 09 '20 at 06:09
2

The $q_i$ are generalized co-ordinates. So $q_1$ might be an angle, and $q_2$ might be a distance. It depends on your particular problem. – Stephen Montgomery-Smith Aug 09 '20 at 06:10

Understanding the SI units of the Euler–Lagrange equation terms

1 Answers1