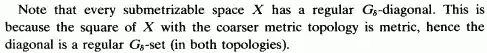Let $M=\mathbb{R}$ and $\tau_M=\{U\cup A: U$ open in $\mathbb{R}, A\subset \mathbb{R} \setminus B\}$, where $B$ is a Bernstein set. Then $(M,\tau_M)$ is a topological space called the Michael Line. It is a regular Lindelof space.
Submetrizable = if we can choose a coarser topology on the space $X$ and thus make it a metrizable space.
Let $f: M \to X$ be any one-to-one and onto continuous mapping. Then is $X$ always submetrizable?
Thanks for your help.
The conjecture fails, because only a “good separated” image $X$ can be submetrizable. It should be (functionally) Hausdorff and have a (regular) $G_\delta$-diagonal. I shall cite the paper [Gru], which deals only with regular spaces.
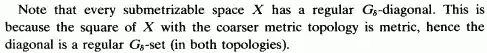
For instance, $\Bbb R\setminus B$ is a uncountable discrete subspace of $M$, so we can weaker its topology to an Aleksandrov compactification of an uncountable discrete space which has uncountable pseudocharacter and so it has no $G_\delta$-diagonal. Also the space $X$ is not Hausdorff, because the compact subset $\Bbb R\setminus B$ is not closed in it.
But if the image $X$ is sufficiently “good separated” then the answer is positive. Namely, if $X$ is a regular space with $G_\delta$-diagonal, it is also paracompact as a regular Lindelöf space and we can apply to it
References
[Gru] Gary Gruenhage. Generalized metric spaces in Handbook of set-theoretic topology, ed. K. Kunen, J. Vaughan, North-Holland, 1984.