2

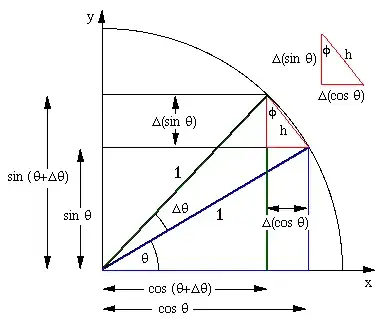
enter image description here

I'm following this post https://math.stackexchange.com/a/2169/612996 as my example and I've figured out how it works for $\sin(\theta)$,

During my first try: I keep on missing the factor of $2$ when it's $\sin(2\theta)$. I always get $\cos(2\theta)$

In my work, I've made the angle $2\theta$ and then changed everything that has $\theta$ to $2\theta$, but I've kept the increase in the angle $\Delta\theta$. I think I could reverse-engineer the answer so I use $\Delta 2 \theta$ and get the right answer, but I don't know why that should work and not $\Delta\theta$ since isn't it just a small increase in the angle anyway? (Or is it a small increase that is relative to the angle, and that's why there's a 2?)

During my second try: I understand the algebraic way of doing the chain rule but I want to do it with some sort of geometric intuition.

  • 1
    Yes, the increase should be relative to the angle. With assuming $\Delta \theta$ as the overall change, you are effectively calculating $d \sin (2\theta) / d(2\theta)$, hence the missing factor of $2$. – Saïd M Aug 02 '20 at 11:34
  • Thanks for the answers, and it's working out in the calculations. I suppose I didn't consider the relative nature of $\Delta \theta$ since I (mistakenly) thought it wasn't going to matter since it was going to zero. But it makes sense in that factored format that the angle change is relative. –  Aug 02 '20 at 11:46
  • @SaMaSo what would the limit of the difference quotient look like? Because it seems like I'll get half of the typical difference quotient, but then I'd be multiplying by 2 (so that it balances out?) –  Aug 02 '20 at 12:08
  • I'm not sure if I understand your question. You have to compute $\frac{ \sin( 2(\theta+\Delta \theta)) - \sin(2\theta)}{\Delta \theta}$. Therefore, when you are considering the right triangle as in the post you linked to, the angle is going from $2\theta$ to $2\theta + 2\Delta\theta$. – Saïd M Aug 02 '20 at 13:38
  • @SaMaSo I think it's because I don't know what the sides of the small similar triangle are. So far I have that for small $\Delta2\theta$, $\cos\left(\phi\right)=\frac{\Delta\sin\left(2\theta\right)}{h} \approx \frac{\sin\left(2\theta+\Delta2\theta\right)-\sin\left(2\theta\right)}{\Delta2\theta}$.And what's on the right is $\frac{d \sin\left(2\theta\right)}{d \left(2\theta\right)}$ –  Aug 02 '20 at 16:06
  • algebraic way? it's really an "analytic way" – zhw. Aug 04 '20 at 21:44

2 Answers2

3

You are taking the derivative with respect to $x$ or $\theta$ not $2 x$ or $2\theta$

So you want $$\frac{d}{d\theta} \sin(2\theta) =\lim\limits_{\Delta \theta \to 0} \frac{\sin(2(\theta+\Delta \theta))-\sin(2\theta) }{\Delta \theta} \\= \lim\limits_{\Delta \theta \to 0} \frac{2\sin\left(\frac{2\theta+2\Delta \theta -2 \theta}{2}\right)\cos\left(\frac{2\theta+2\Delta \theta +2 \theta}{2}\right) }{\Delta \theta} \\= \lim\limits_{\Delta \theta \to 0} \frac{2\sin\left(\Delta\theta\right)\cos\left(2\theta+\Delta \theta\right) }{\Delta \theta}\\= \lim\limits_{\Delta \theta \to 0} \frac{2\Delta\theta\cos\left(2\theta\right) }{\Delta \theta} \\=2 \cos(2\theta)$$

Henry
  • 157,058
  • I like very much...approved...:-) – Sebastiano Aug 02 '20 at 21:10
  • Thanks, but I'm still wondering how you'd get that from the picture seen here https://math.stackexchange.com/a/2169/751840 . I understand using a trig identity to solve it algebraically, but I'm seeing if I can understand chain rule by pictures alone. If in that picture, $\theta$ changes to $2\theta$, then we should be able to derive chain rule from that. –  Aug 03 '20 at 00:19
  • @ Sat: You want to geometrically show that:$\dfrac{d\sin(2\theta) }{d\theta} =2 \cos(2\theta).$ right? – Narasimham Aug 05 '20 at 15:48
  • @Narasimham yeah. I want to use the same picture to show but have the correct outcome. –  Aug 06 '20 at 16:13
  • @Sebastiano how does the second line relate to the picture, or if it's an trigonometric identity, how would you know to use it. –  Aug 09 '20 at 01:51
  • @Henry, I get it! :D After looking up identities, you used a "Sum-to-Product" formula and it works out nicely. Although it's not as geometric as I'd like, it's good enough for me since I could recreate the answer for myself now. (I guess I should really refresh and relearn my trig identities). –  Aug 10 '20 at 05:15
1

In your picture, you want to change all the $\theta$'s into $2\theta$'s, right? Then the whole argument for $\sin \theta$ goes through, but instead for $\sin 2\theta$; especially you have $\Delta 2\theta$ instead of $\Delta \theta.$

So if $\theta$ increases by $\Delta \theta$, what is the increase in $\Delta 2\theta$? Answer: It's $2\Delta\theta.$ So I think that your sticking point comes down to:

$$\Delta 2\theta = 2\Delta \theta.$$

B. Goddard
  • 1
  • Yes, I think I get that now. I'm still having trouble figuring how to process the numerator. I see Henry's answer above and although it makes sense algebraically, I'm not sure how he saw it, or how it relates to the picture. It doesn't look like the obvious thing to do. –  Aug 09 '20 at 01:49