First, take some definition: Given a topological space 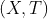 and net, defined on
and net, defined on 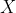 :
: 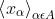 . We say that x is cluster point of
. We say that x is cluster point of 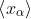 net, if for every
net, if for every  open set and for every
open set and for every  , there exist
, there exist 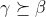 , such that
, such that 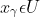 .
.
We know that sequence is a special kind of net. Also, every subsequence is subnet, but all subnet is not a subsequence.
It is known the theorem: Given a arbitrary topological space and net on it. than, x is the cluster point of the net if and only if, there exist subnet of the net, which converges to x.
This theorem is true if the net is sequence (as net). This means, that is there exist subsequence, which is converges to x, than there exist subnet, that converges to x (because subsequence is a subnet) and than x is the cluster point of the sequence (as net). But, conversely we cant say, that if x is the cluster point then there exist subsequence, that is converges (by theorem, where exist subnet but we dont know that this subnet is a subsequence). But it is easy to prove, that if topological space is first countable, than there exist a convergence subsequence also.
I want to find topological space (of cource, it would be not first countable) and sequcence on it, which has a cluster point (x), but there is not subsequence which is converges to x.