I have some basic question with polynomials appreciate if someone could explain me this.
Following is additional and multiplication tables and it is say that this is a field. Have no idea why say it is field.
Please explain me.
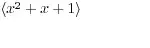
I have some basic question with polynomials appreciate if someone could explain me this.
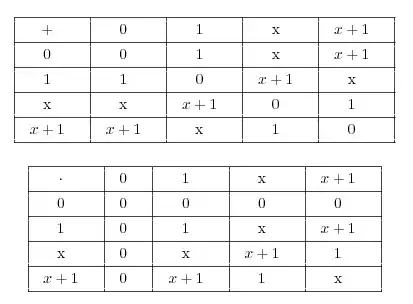
Following is additional and multiplication tables and it is say that this is a field. Have no idea why say it is field.
Please explain me.
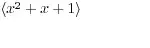

Just note that, for multiplication, every non-zero element on the first column has, on its line, a $1$, which means it has a inverse to the right... Now, for every element on the first row, which contains nonzero elements, it has a 1 on its column, which means it is left-invertible.
Thus, it is a field since every nonzero element is invertible.
If $R$ is a ring with unity and $f\in R[x]$ a polynomial, then $R[x]/\langle f\rangle$ is always at least a ring. To be a field, it needs a unity (check) and each nonzero element must have a multiplicative inverse (check).
Similar to the answer of Hagen von Eitzen above (I credit his work), it is a well-known result if $F$ is a field, then $F[x]$ is Euclidean domain. And (given a irreducible polynomial (irreducible in F[x]), say $r(x)$ in $F[x]$) if $D=F[x]/<r(x)>$, then $D$ is a field. As a example, $R[x]/<x^2+1>$ is field (can you see which field)? Now, for proving the final result, all that we need to prove is (over $F_2$), $x^2+x+1$ is irreducible. As $x^2+x+1$ is a degree $2$ polynomial, we merely need to show $x^2+x+1$ has (in $F_2$) no roots. Thus...