6

I saw this post but it was too technical for me.

I am looking for proof similar to what is shown in this Quora post by Nicholas Halderman. The part I found confusing/ hard of the proof was where he proves the lemma:'a small displacement in this direction along this curve will result in a point closer to B.', I am looking for alternate geometric proof/ a more elaborate explanation on what he has done in the post.

tryst with freedom
  • 11,538
  • Do you understand why the shortest distance between two straight lines is along a common normal? The proof is almost the same since the curves are almost straight near the points. – Chrystomath Jul 27 '20 at 09:02
  • Hm, that thing I understood through algebra but I'd be interested ina geometric proof of that as well – tryst with freedom Jul 27 '20 at 09:06
  • @DDD4C4U I think several people already told you about this. Please pay more attention to punctuation. All sentences should finish with a full stop. Sloppiness like this is turning people off. – PatrickR Aug 06 '20 at 03:48
  • My English is not very strong but I tried improving the post c: – tryst with freedom Aug 06 '20 at 09:01

3 Answers3

6

A geometric argument, assuming that a shortest segment exists:

Take any point $A$ on the first curve $\gamma_1$. In order to find the point nearest to $A$ on the second curve $\gamma_2$ draw a small circle centered at $A$ and blow it up until it meets, in fact touches, the second curve $\gamma_2$ at some point $A'$. From all points on $\gamma_2$ this point $A'$ is nearest to $A$. The segment $A A'$ is a radius of the circle, hence orthogonal to the common tangent of the circle and $\gamma_2$ at $A'$.

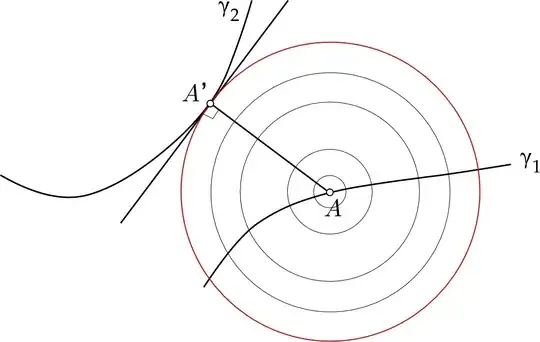
enter image description here

Of course this works also in the other direction. It follows that for any segment from $\gamma_1$ to $\gamma_2$ that is not orthogonal on both curves the above circle construction finds a shorter one.

Christian Blatter
  • 226,825
2

If curves are continuous and differentiable, take parametrizations $c_1(t)$ and $c_2(s)$ of the curves. We know that at the minimum points of the squared distance $\|c_1(t) - c_2(s)\|^2$ the derivative in each variable will be $0$. We get

$$ \frac{d}{dt}\|c_1(t) - c_2(s)\|^2 = 2(c_1(t) - c_2(s))\cdot c_1'(t) = 0 $$ That is, the points minimizing the distance satisfy $c_1(t) - c_2(s)$ being normal to $c_1'(t)$, which is parallel to the curve $c_1$ at $c_1(t)$. The same argument deriving the formula above for $s$ will show that $c_1(t) - c_2(s)$ is also normal to $c_2$ at $c_2(s)$.

MBW
  • 613
  • did you use dot product or something? how did u get that it's normal – tryst with freedom Jul 27 '20 at 11:33
  • @DDD4C4U If $f(t) : \mathbb{R} \rightarrow \mathbb{R}^n$, then $\frac{d}{dt}| f(t) | ^2 = \frac{d}{dt}(f(t) \cdot f(t)) = 2f(t)\cdot f'(t)$ where $a\cdot b$ is the dot product, yes. The dot product is zero when the vectors are normal to each other – MBW Jul 27 '20 at 12:10
  • "We know that at the minimum points of the squared distance $|c_1(t) - c_2(s)|^2$ the derivative in each variable will be $0$." Or it occurs in the endpoints of the curves. Or the minimum doesn't exist. – Michael Hoppe Jul 27 '20 at 13:25
  • @MichaelHoppe indeed. I implicitly excluded these case by assuming such a point exists and derivatives exist at that point, but yes, my answer would make no sense otherwise. I figured I would do it implicitly as the question also implicitly states in are in this case. – MBW Jul 27 '20 at 14:17
  • I am not very familar where the magnitude gives you dot product gives you a dot product of vectors, is there a name to this? – tryst with freedom Jul 27 '20 at 18:27
  • @DDD4C4U check this here: https://en.wikipedia.org/wiki/Dot_product#Geometric_definition – MBW Jul 27 '20 at 20:59
  • Ah some months later and I finally understand your answer. Good one! – tryst with freedom Dec 03 '20 at 21:55
1

Take curves $\gamma_1,\gamma_2$ and let the points at minimum distance be $P_1,P_2$.

Suppose the tangents to $\gamma_1$ at $P_1$ and to $\gamma_2$ at $P_2$ are not parallel. Then they meet somewhere; let's say they meet further to the "left" along each tangent. That means we can draw parallel lines $\ell_1$ through $P_1$ and $\ell_2$ through $P_2$, such that as you go to the "left", the tangents are closer than $\ell_1$ and $\ell_2$. But points on $\gamma_1$ sufficiently close to $P_1$ are the same side of $\ell_1$ as the tangent is, and similarly for $\gamma_2$, meaning that going a small distance along each curve to the "left" gives two points which are closer together.

Now suppose the tangents are parallel but the normals do not coincide. Say the line segment $P_1P_2$ is to the "left" of the normal to $\gamma_1$ at $P_1$, and so to the "right" of the normal to $\gamma_2$ at $P_2$. Now we can draw parallel lines $\ell'_1,\ell'_2$ through $P_1$ and $P_2$ which are perpendicular to $P_1P_2$, and if we move a small amount to the "left" of $P_1$ along $\ell'_1$ and to the "right" of $P_2$ along $\ell'_2$, we get closer together. But as we move "left" from $P_1$ the tangent lies on the side of $\ell'_1$ which is closer to $\ell'_2$ and similarly for moving "right" from $P_2$. Since the curves lie between the tangents and $\ell'_1,\ell'2$ if we move a sufficiently small distance, this means they are even closer together.

Especially Lime
  • 40,828