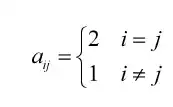0

I've received an assignment to solve the following determinant for the matrix:

A is an nxn matrix defined as follows:

enter image description here

Show that the determinant of A is equal to n+1.

I've tried solving it and got stuck, so I checked the solution:

enter image description here

I'm just puzzled, how did the transition from the first determinant to the second happen? I thought maybe they added all the rows to the first one, but it doesn't make sense to me because they received the same result in every variable.

Help would be much appreciated!

RandyMarsh
  • 85
  • When the whole row (or column) becomes k times, the determinant also becomes k times. (You could confirm this with a simple 2 x 2 matrix.) The solution adds all of the n rows to form the 1st row of the second matrix in the solution. (The (n-1) 1's and 1 2's add up to n+1 for every column.) Also, since we could factor n+1 out of the first row, the determinant would become 1/(n+1) times, and therefore the (n+1) sort of 'factors out' of the matrix. The rest solution is adding some row to the appropriate row, which does not change the determinant. Hope it helps :) – Joshua Woo Jul 26 '20 at 09:02
  • Your guess is correct. I don't really understand your objection: ‘they received the same result in every variable’ . Which variable? – Bernard Jul 26 '20 at 09:07
  • https://math.stackexchange.com/questions/84206/how-to-calculate-the-determinant-of-all-ones-matrix-minus-the-identity – Angina Seng Jul 26 '20 at 09:07
  • Ohh now I see, I forgot about the fact that each column has 2 inside it, and eventually the sum is the same. Thanks for the help mates! – RandyMarsh Jul 26 '20 at 09:10

0 Answers0