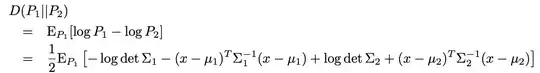0

A probability measure is typically defined as a function $\mathbb{P}: \mathcal{F} \rightarrow [0, 1]$, where $\mathcal{F}$ is a $\sigma$-algebra, i.e. a set of events (which are themselves sets of outcomes), so $\sigma$-algebras are sets of sets.

Now, it's often the case that one defines the Gaussian p.d.f. (or just Gaussian function, i.e. an exponential function) as follows

$$ p(x)=\frac{1}{(2 \pi)^{n / 2} \operatorname{det}(\Sigma)^{1 / 2}} \exp \left(-\frac{1}{2}(x-\mu)^{T} \Sigma^{-1}(x-\mu)\right) $$

When I look at this expression, I think that $x$ is a dummy variable. Now, there are cases where one needs to compute something as a function of a "distribution" (which I assume they mean "probability measure"), e.g. the KL divergence is an example of a function between probability measures, but then the Gaussian p.d.f.s are used to actually compute the KL divergence. Now, I know we can also define the KL divergence between p.d.f.s, but, in the derivation of these notes, the author writes

enter image description here

So, he defines the KL divergence $D$ between probability measures (or distributions or whatever they are) $P_1$ and $P_2$ and then he uses the definition of the Gaussian p.d.f. Note that he just took the logarithm of the exponential function, and that should explain the last term there. Now, you can see that this KL divergence is an EXPECTATION. Now, expectations are operators, i.e. functions that take functions, and, more precisely, expectations take random variables as inputs (as far as I know), so the expression inside the expectation

$$ -\log \operatorname{det} \Sigma_{1}-\left(x-\mu_{1}\right)^{T} \Sigma_{1}^{-1}\left(x-\mu_{1}\right)+\log \operatorname{det} \Sigma_{2}+\left(x-\mu_{2}\right)^{T} \Sigma_{2}^{-1}\left(x-\mu_{2}\right) $$

must be a random variable. Given that $\mu_1, \mu_2, \Sigma_1$ and $\Sigma_2$ are constants, $x$ must be the (basic?) random variables. However, above, when we defined the Gaussian pdf, $x$ was a dummy variable (I guess). So, it's not clear what's going on here. First, we have a pdf and then the pdf is a random variable. Can someone clarify this to me? What's being used then to compute the KL divergence? p.d.f.s or random variables? I think they must be random variables, because the KL divergence is defined as an expectation, but then I don't understand the relationship between the Gaussian random variable $p(x)$ and the Gaussian p.d.f. $p(x)$. Is a Gaussian r.v. just defined as a Gaussian p.d.f. where the $x$ is r.v. from the sample space to another measurable space (which one?)?

1 Answers1

1

In those notes, $P_1,P_2$ are probability densities, not measures. If we write this more conventionally using upper case to denote probability measures and lower case for the corresponding densities, it would be
$$D(P_1\parallel P_2) = \int_{-\infty}^\infty p_1(x)\log {p_1(x)\over p_2(x)}\, dx,$$ where, as you noted, $x$ is just a "dummy" variable.

Note that this quantity, and the densities themselves, need not be seen as involving the concept of "random variable" at all, since the basic probability space can be taken as $(\mathbb{R},\mathcal{B}(\mathbb{R}),P).$ (In this context, a density $p$ corresponding to probability measure $P$ is any nonnegative function such that for every set $A\in\mathcal{B}(\mathbb{R})$, we have $P(A)=\int_A p(x)\, dx$ -- nothing about random variables.)

However, if we define the identity function $X:\mathbb{R}\to\mathbb{R}:x\mapsto x$, then $X$ is a $(\mathbb{R},\mathcal{B}(\mathbb{R}))$-measurable function, i.e. a random variable, and we can write the previous expression as an expectation: $$D(P_1\parallel P_2) = E_{P_1}\log {p_1(X)\over p_2(X)}$$ where the subscript indicates that $P_1$ is to be assumed for the underlying probability space, hence also the probability measure induced by $X$. (This is where those notes got sloppy by using the same notation for both the random variable and the "dummy" variable.)

r.e.s.
  • 14,371
  • I don't understand this notation $X:\mathbb{R}\to\mathbb{R}:x\mapsto x$. What does it mean? Are you composing functions? Which functions are you compositing and what is their definition? –  Jul 26 '20 at 12:52
  • @nbro $g:A\to B:x\mapsto g(x)$ is a fairly standard notation that means "$g$ is a function from $A$ to $B$ that maps element $x$ to element $g(x)$". (Here $X$ is just the identity function, mapping each element to itself.) See https://en.wikipedia.org/wiki/Function_(mathematics)#Arrow_notation – r.e.s. Jul 26 '20 at 13:05
  • I don't really understand the purpose of this. Does this mean that, if $f$ is the pdf of some random variable $Z$, then $f(Z)$ is also a function $\mathbb{R} \rightarrow \mathbb{R}: x \mapsto x$? I don't think so, it should be a function of the form $\Omega \rightarrow \mathbb{R}$, but then why can we do $p_1(X)$ (which is a function from $\Omega$ to $\mathbb{R}$) as you suggest? Also, what's the relationship between $p_1$ and your defined $X$? How come that this r.v. $X$ is associated with $p_1$? –  Jul 26 '20 at 13:14
  • @nbro No, it means that if there is Gaussian distribution on the measure space $(\Omega,\mathcal{F})=(\mathbb{R},\mathcal{B}(\mathbb{R}))$, then the identity function on $\Omega$ is a random variable with a Gaussian pdf. A r.v. is not needed to define the Gaussian distribution. – r.e.s. Jul 26 '20 at 13:17
  • Well, but I want to understand WHY we can really use $p_1(X)$, where $p_1$ is a pdf and $X$ is its random variable, and what is its meaning. As far as I understand, you have not explained it yet. I also don't understand why you invented this new random variable $X$. –  Jul 26 '20 at 13:22
  • @nbro Here $p_1=p_1\circ X$ (function composition) because $X$ is defined as the identity function on $\Omega(=\mathbb{R})$. What more is there to explain? (The r.v. $X$ is invented so we can write the integral as an expectation.) – r.e.s. Jul 26 '20 at 13:30
  • Is your defined $X$ an r.v. that has density $p_1$ or not? –  Jul 26 '20 at 13:33
  • Let us continue this discussion in chat. – r.e.s. Jul 26 '20 at 13:35