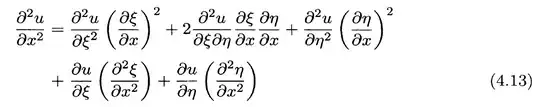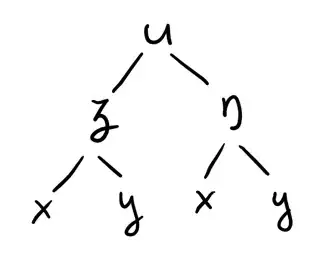5

I've been stuck on this for a couple of days. So this is from this book ("Partial Differential Equations in Mechanics 1", page 125).

Book cover: Partial Differential Equations in Mechanics 1

Section 4.2 Reduction to canonical forms, which leads to the development of the Laplace equation.

In this section, I don't understand how they expand the second-order partial derivative:

Formula of second-order derivative of u w.r.t. x

Where,

Exert from page 125.

Here is what I got so far. When I do it, I only get to have 4 terms, and not 5 like what's in the book. Here I apply product rule first and then the chain rule (Note, I'm using square brackets to indicate that I am taking the partial derivative of whatever is in them. Just to keep it organized).

$$\begin{align} \frac{\partial}{\partial x}\frac{\partial u}{\partial x} &= \\ &= \frac{\partial}{\partial x} \biggl( \frac{\partial u}{\partial \xi} \frac{\partial \xi}{\partial x} + \frac{\partial u}{\partial \eta} \frac{\partial \eta}{\partial x} \biggr) \\ &=\frac{\partial}{\partial x} \biggl( \frac{\partial u}{\partial \xi} \frac{\partial \xi}{\partial x}\biggr) + \frac{\partial}{\partial x} \biggl(\frac{\partial u}{\partial \eta} \frac{\partial \eta}{\partial x} \biggr) \\ &= \frac{\partial}{\partial x} \biggl[ \frac{\partial u}{\partial \xi} \biggr] \frac{\partial \xi}{\partial x} + \frac{\partial u}{\partial \xi} \frac{\partial}{\partial x} \biggl[ \frac{\partial \xi}{\partial x} \biggr] + \frac{\partial}{\partial x} \biggl[ \frac{\partial u}{\partial \eta} \biggr] \frac{\partial \eta}{\partial x} + \frac{\partial u}{\partial \eta} \frac{\partial}{\partial x} \biggl[ \frac{\partial \eta}{\partial x} \biggr] \\ \text{Now the chain rule:}\\ &= \frac{\partial}{\partial \xi}\biggl[\frac{\partial u}{\partial \xi}\biggr] \frac{\partial \xi}{\partial x} \frac{\partial \xi}{\partial x} + \frac{\partial u}{\partial \xi} \frac{\partial^2 \xi}{\partial x^2} + \frac{\partial}{\partial \eta}\biggl[\frac{\partial u}{\partial \eta}\biggr] \frac{\partial \eta}{\partial x} \frac{\partial \eta}{\partial x} + \frac{\partial u}{\partial \eta} \frac{\partial^2 \eta}{\partial x^2} \\ &=\frac{\partial^2 u}{\partial \xi^2} \biggl(\frac{\partial \xi}{\partial x} \biggr)^2 + \frac{\partial u}{\partial \xi} \frac{\partial^2 \xi}{\partial x^2} + \frac{\partial^2 u}{\partial \eta^2} \biggl(\frac{\partial \eta}{\partial x} \biggr)^2 + \frac{\partial u}{\partial \eta} \frac{\partial^2 \eta}{\partial x^2} \end{align} $$ My tree of the chain rule looks like this (is it correct?)

hand drawn tree of the chain rule of u

In addition, if someone could explain why this chain rule is valid? Granted, this may be a whole topic on its own, so if you could just point to some resource or what this particular operation is called, that would do.

$$ \frac{\partial}{\partial x}\biggl[ \frac{\partial u}{\partial \xi} \biggr] = \frac{\partial}{\partial \xi} \biggl[\frac{\partial u}{\partial \xi}\biggr]\frac{\partial \xi}{\partial x} $$

Thank you in advance.

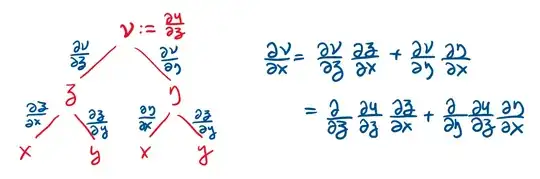
UPDATE:

(as per answer by @peek-a-boo)

chain rule tree of second order derivative of u wrt x

P.S. Corrections or edits are welcomed.

Jek Denys
  • 139

1 Answers1

3

You have a mistake when calculating $\dfrac{\partial}{\partial x}\left[\dfrac{\partial u}{\partial \xi}\right]$ and $\dfrac{\partial}{\partial x}\left[\dfrac{\partial u}{\partial \eta}\right]$ in the middle where you're missing a extra step in the chain rule. For simplicity, just call $v:= \dfrac{\partial u}{\partial \xi}$. Then by equation (4.11), we have \begin{align} \dfrac{\partial v}{\partial x} &= \dfrac{\partial v}{\partial \xi} \dfrac{\partial \xi}{\partial x} + \dfrac{\partial v}{\partial \eta} \dfrac{\partial \eta}{\partial x}. \end{align} So, if we plug in the definition of $v$, we get \begin{align} \dfrac{\partial}{\partial x}\left[\dfrac{\partial u}{\partial \xi}\right] &= \dfrac{\partial^2 u}{\partial \xi^2} \dfrac{\partial \xi}{\partial x} + \dfrac{\partial^2 u}{\partial \eta \partial \xi} \dfrac{\partial \eta}{\partial x}. \end{align} Similarly, \begin{align} \dfrac{\partial}{\partial x}\left[\dfrac{\partial u}{\partial \eta}\right] &= \dfrac{\partial^2 u}{\partial \xi \partial \eta} \dfrac{\partial \xi}{\partial x} + \dfrac{\partial^2 u}{\partial \eta^2} \dfrac{\partial \eta}{\partial x}. \end{align} Finally, when you put all of this together, just remember that mixed partial derivatives are equal: $\dfrac{\partial^2 u}{\partial \xi \partial \eta} = \dfrac{\partial^2 u}{\partial \eta \partial \xi}$ (that's how the factor of $2$ comes up in equation $4.13$)

And yes, your chain rule tree looks right (that's how you can get 4.11 and 4.12). You can also create similar chain-rule trees for $\frac{\partial u}{\partial \xi}$ and $\frac{\partial u}{\partial \eta}$. As for why the chain rule is valid... well that's a completely different issue, which you should probably ask in a separate question if this answer isn't sufficient.

peek-a-boo
  • 55,725
  • 2
  • 45
  • 89
  • That's a great looking answer. Thank you! Except, I don't understand the "for simplicity" part. Is it possible to write it without the simplicity, just bare, raw, non-shortened, as-is form? – Jek Denys Jul 25 '20 at 19:35
  • I'm just getting confused with the assignment to $\nu$. If it's the partial derivative of u w.r.t. $\xi$, why is there $\eta$ ? – Jek Denys Jul 25 '20 at 19:41
  • @JekDenys I mean if you want to avoid the "for simplicity" then ignore the first equation, and go directly to the second equation. All we're doing is applying equation 4.11 to $\dfrac{\partial u}{\partial \xi}$ instead of $u$. The issue you seem to be having is that you're not comfortable with applying equation 4.11 to other functions. The thing is equation 4.11 is valid for ANY function of $\xi,\eta$, so I can apply it first to $u$, then to $\dfrac{\partial u}{\partial \xi}$, then I can apply it to $\dfrac{\partial ^4u}{\partial \xi^2 \partial \eta^2}$ or literally any other function. – peek-a-boo Jul 25 '20 at 20:05
  • 1
    The general rule is $\dfrac{\partial (\text{function})}{\partial x} = \dfrac{\partial (\text{function})}{\partial \xi}\dfrac{\partial \xi}{\partial x}+ \dfrac{\partial (\text{function})}{\partial \eta}\dfrac{\partial \eta}{\partial x}$... this is exactly what the chain rule of multivariable calculus says. You can literally plug in any function of $(\xi,\eta)$. – peek-a-boo Jul 25 '20 at 20:10
  • O-oh, I think I got it. I've updated my question with the tree for the chain rule of second-order (is it correct?). Can you just clarify, why, if $\nu$ is a derivative or u w.r.t. $\xi$, why do we include the $\eta$ components? – Jek Denys Jul 25 '20 at 20:22
  • 1
    @JekDenys $v = \dfrac{\partial u}{\partial \xi}$, but this is still a function of two variables. More precisely, $v(\xi,\eta) := \dfrac{\partial u}{\partial \xi}(\xi,\eta)$. THis is one of the very hige pitfalls of Leibniz notation where you don't explicitly mention where the functions and derivatives are being evaluated. Because this is a function of $(\xi,\eta)$, you still need to take partial derivatives with respect to $\xi$ AND $\eta$ when applying the chain rule – peek-a-boo Jul 25 '20 at 20:24
  • Btw, what notation would be better for this? – Jek Denys Jul 25 '20 at 20:32
  • @JekDenys "better" is subjective. There are two ways of judging "better". The first is the "proper, no nonsense" way, which is extremely precise in notation, but very tedious and cumbersome to write out (but if you want to know exactly what your theorems are talking about, then of course you need to clarify all these details). The second is "more convenient, but slightly sloppy" (Leibniz notation, which you should use only if you know what you're doing, but often it is much easier and quicker to write). – peek-a-boo Jul 25 '20 at 20:36
  • It's kind of like when you first learn grammar (I'm not sure if this is the best analogy but whatever), you "do things by the book", but as you get more familiar, you tend to be much looser with the details because we generally know what's going on, and if need be, we can certainly make things more "formal, proper and unambiguous". Anyway, here's an answer I wrote a while back, and at this point it may or may not be helpful for you; I'm not sure. But if at some future point you get confused by the various chain rules, you may find it helpful. – peek-a-boo Jul 25 '20 at 20:38
  • 1
    If it were me then because I've practiced several times with "translating" between the precise and sloppy versions, I would opt for the more convenient option and write things as in the book (but I would do this only because I know exactly how to write all of this in more precise notation if the need arises). But of course, it is a good test of your understanding to see if you can write the same thing in both ways, and see how the two notations differ. – peek-a-boo Jul 25 '20 at 20:43