What is the problem with this method while integrating $(e^x-(2x+3)^4)^3$?
I already know what is its integration. I collected the answers from Quora (black ones) and WolframAlpha website (the red one).
Alright, then I tried to solve the integration in this method. But, the answer appeared different. The mathematical approach seemed very legitimate to me. Where did I go wrong, would you kindly point that out?
here's my answer
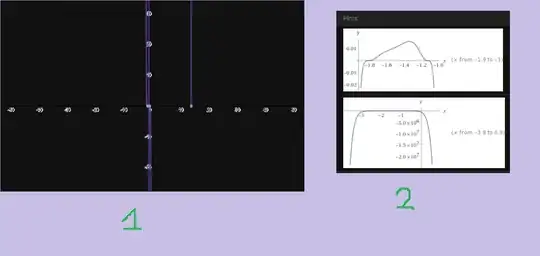
now here is the difference between my itegrals(1) graph and the graph that gave wolphrapalpha(2).
I used same method to solve this two functions i found. and it worked.
BUT WHY IT DID NOT WORK FOR THAT ONE, WHERE DID I WENT WRONG?