Generating Function for sum of N dice [or other multinomial distribution] where lowest N values are "dropped" or removed

Question

I came across this interesting question on another StackExchange sub that has not been answered after a couple of years. After searching Meta for protocol and finding this post, I think it's appropriate to cross-post here.

I have duplicated the original question verbatim below.

Background

I found this interesting question https://stats.stackexchange.com/questions/130025/formula-for-dropping-dice-non-brute-force/242839 and excellent answer https://stats.stackexchange.com/a/242857/221422, but couldn't figure out how to generalize a generating function for when more than one die is dropped. Similarly, I'm having difficulty figuring out a related mechanic for when the highest roll is dropped.

Description of the Problem

Suppose you have $N$ fair dice each with $S$ sides. Roll all the dice and then remove the lowest [or highest, alternatively] $M$ (where $M > 0$ and $M < N$) dice and then sum the remainder. What is the probability distribution of the sum? Specifically, how does one go about finding the generating polynomial?

Implementation of whuber's answer

I found whuber's answer to be incredibly thorough. I thought it might be nice to see how to actually implement it in code, so I've pasted that below.

from functools import reduce

from numpy.polynomial import polynomial as p


def generating_function(k, d, n):
    return p.polypow(
        [0] * k + [1] * (d - k + 1),
        n
    )


def drop_one_die(n, d):
    tmp = [
        generating_function(k, d, n) for k in range(1, d + 2)
    ]

    differences = (
        (tmp[i] - tmp[i + 1])[i + 1:] for i in range(d)
    )

    return reduce(p.polyadd, differences)


print(
    drop_one_die(4, 6)
)

Other considerations / Multinomial distribution

To generalize even further, instead of a fair die where each outcome is equally likely, what if you start with a general multinomial distribution?

So instead of

$$(1/6)x + (1/6)x^2 + (1/6)x^3 + (1/6)x^4 + (1/6)x^5 + (1/6)x^6$$

you start with

$$p_0 + {p_1}{x} + {p_2}{x^2} + ... + {p_n}{x^n}$$

Thanks!

Answer 1

(answer completed)

1. Premise

The number of ways to throw $m$ fair dies, with faces numbered $[1,R]$ and obtaining a sum $S$ corresponds to $$ \eqalign{ & {\rm No}{\rm .}\,{\rm of}\,{\rm solutions}\,{\rm to}\;\left\{ \matrix{ {\rm 1} \le {\rm integer}\;f_{\,j} \le R \hfill \cr f_{\,1} + f_{\,2} + \; \cdots \; + f_{\,m} = S \hfill \cr} \right.\quad \Rightarrow \cr & \Rightarrow \quad {\rm No}{\rm .}\,{\rm of}\,{\rm solutions}\,{\rm to}\;\left\{ \matrix{ {\rm 0} \le {\rm integer}\;x_{\,j} \le R - 1 = r \hfill \cr x_{\,1} + x_{\,2} + \; \cdots \; + x_{\,m} = S - m = s \hfill \cr} \right. \cr} $$ and it is convenient to consider the problem in the second version given above as:

Number of ways to throw $m$ fair dies, with faces numbered $[0,r]$ and obtaining a sum $s$

That number is given by $$ \bbox[lightyellow] { \eqalign{ & N_b (s,r,m) = \cr & = {\rm No}{\rm .}\,{\rm of}\,{\rm solutions}\,{\rm to}\;\left\{ \matrix{ {\rm 0} \le {\rm integer}\;x_{\,j} \le r \hfill \cr x_{\,1} + x_{\,2} + \; \cdots \; + x_{\,m} = s \hfill \cr} \right.\quad = \cr & = \left\{ {\matrix{ {\sum\limits_{\left( {0\, \le } \right)\,\,k\,\,\left( { \le \,{s \over {r + 1}}\, \le \,m} \right)} {\left( { - 1} \right)^k \binom{m}{k} \binom{ s + m - 1 - k\left( {r + 1} \right) }{ s - k\left( {r + 1} \right)}} } & {0 \le {\rm integers}\;s,r,m} \cr {\rm 0} & {{\rm otherwise}} \cr } } \right. \cr} \tag{1}}$$ as explained in this post.
I took the liberty to change your notation for keeping congruent with previous posts on the subject.

Among the various properties of $N_b$ let's cite
symmetry $$ N_b (mr - s,r,m) = N_b (s,r,m) $$ ogf $$ F_b (x,r,m) = \sum\limits_{0\,\, \le \,\,s\,\,\left( { \le \,\,r\,m} \right)} {N_b (s,r,m)\;x^{\,s} } = \left( {1 + x + \cdots + x^{\,r} } \right)^m = \left( {{{1 - x^{\,r + 1} } \over {1 - x}}} \right)^m $$ sum $$ \sum\limits_{\left( {0\, \le } \right)\,\,s\,\,\left( { \le \,mr} \right)} {N_b (s,r,m)} = (r + 1)^{\,m} =F_b (1,r,m) $$

2. Histogram representation

For our scope it is convenient to introduce the equivalence of the dice sum with
Number of ways to lay $s$ undistinguishable balls into $m$ distinguishable bins, each with max capacity $r$
and in particular with
Number of histograms with $m$ bars of height $[0,r]$, summing to $s$

3. Extending the definition of $N_b$ and $F_b$

In the steps to follow it is of advantage to slightly modify the definition of $N_b$ and $F_b$ in order to allow $r$ to take negative values: $$ \bbox[lightyellow] { \left\{ \matrix{ F_{\,b\, * } (x,r,m) = \left[ {r < 0} \right]\left[ {0 = m} \right] + \left[ {0 \le r} \right]\left( {1 + x + \cdots + x^{\,r} } \right)^m \hfill \cr N_{\,b\, * } (s,r,m) = \left[ {r < 0} \right]\left[ {0 = m} \right]\left[ {0 = s} \right] + \left[ {0 \le r} \right]N_b (s,r,m) \hfill \cr} \right. \tag{3}}$$ where $[P]$ denotes the Iverson bracket

4. Decomposition into bins filled below, equal and above a threshold

Consider the following decomposition of $F_{b*}$ $$ \bbox[lightyellow] { \begin{array}{l} F_{b*} (x,r,m) = \left( {1 + x + \cdots + x^{\,r} } \right)^m = \\ = \left( {1 + x + \cdots + x^{\,t - 1} + x^{\,t} + x^{\,t + 1} + \cdots + x^{\,t + \left( {r - t} \right)} } \right)^m = \\ = \sum\limits_{\left\{ {\begin{array}{*{20}c} {0\, \le \,a,b,c} \\ {a + b + c\, = \,m} \\\end{array}} \right.} {\left( \begin{array}{c} m \\ a,b,c \\ \end{array} \right) \left( {\frac{{1 - x^{\,t} }}{{1 - x}}} \right)^{\;a} x^{\,b\,t} \left( {x^{\,t + 1} \frac{{1 - x^{\,r - t} }}{{1 - x}}} \right)^{\,c} } = \\ = \sum\limits_{\left\{ {\begin{array}{*{20}c} {0\, \le \,a,b,c} \\ {a + b + c\, = \,m} \\\end{array}} \right.} {\left( \begin{array}{c} m \\ a,b,c \\ \end{array} \right) F_{b*} (x,t - 1,a)\,x^{\,b\,t} x^{\,c\,\left( {t + 1} \right)} F_{b*} (x,r - t - 1,c)} = \\ = \sum\limits_{\left\{ {\begin{array}{*{20}c} {0\, \le \,b,c} \\ {0\, \le \,b + c\, \le \,m} \\\end{array}} \right.} {\left( \begin{array}{c} m \\ b + c \\ \end{array} \right) \left( \begin{array}{c} b + c \\ c \\ \end{array} \right) F_{b*} (x,t - 1,m - \left( {b + c} \right))\,x^{\,\left( {b + c} \right)\,t} x^{\,c\,} F_{b*} (x,r - t - 1,c)} = \\ = \sum\limits_{\left( {0\,\, \le } \right)\,\,q\,\,\left( { \le \,\,m} \right)} {\left( \begin{array}{c} m \\ q \\ \end{array} \right)\,x^{\,q\,t} \, F_{b*} (x,t - 1,m - q)\sum\limits_{\left( {0\,\, \le } \right)\,\,c\,\,\left( { \le \,\,q} \right)} {\left( \begin{array}{c} q \\ c \\ \end{array} \right)x^{\,c\,} F_{b*} (x,r - t - 1,c)} } = \\ = \sum\limits_{\left( {0\,\, \le } \right)\,\,q\,\,\left( { \le \,\,m} \right)} {\left( \begin{array}{c} m \\ q \\ \end{array} \right)\,x^{\,q\,t} \, F_{b*} (x,t - 1,m - q)\left( {1 + x\frac{{1 - x^{\,r - t} }}{{1 - x}}} \right)^{\,q} } = \\ \quad \quad \vdots \\ back\;to\;start\; \\ \end{array} \tag{4}}$$ clearly it represents a partition of the histograms with
$a$ bins filled with less than $t$ balls,
$b$ bins filled with exactly $t$ balls,
$c$ bins filled with more than $t$ balls;
where of course $a+b+c = m$ and where $t$ is any fixed threshold between $0$ and $r$.

The presence of $t-1$ and $r-t-1$ is the motivation for using the extended definition, which allows to uniformly cover the case in which they are negative.

The extraction of the coefficents in terms of the respective $N_{b*}$ is quite straightforward.

5. solution of the problem

Using the building blocks above, we come now to solve the proposed problem, that we can translate as
given all the histograms with $m$ bins of capacity $[0,r]$, upon that we delete $d$ bins with highest filling and sum the remaining, how many histograms will there be with a given residual sum $w$ ?

If $d=0$ we already have the answer.
For $1 \le d$ the deleted bins will have a minimum content that we denote as $u$, and there should be at least one deleted bin with that content.
The minimum $u$ itself, in case together with the number $b$ of bins filled at $u$, will individuate a partition of all the histograms before and upon deletion.

So we retake the situation at the para. above with $a,b,c$ indicating the number of bins $ <, \; = ,\; > \; u$ before the deletion.
Then the $d$ deleted bins shall be the total of the $c$ plus at least one of the $b$.
That is we shall have $$ \left\{ \matrix{ a + b + c = m \hfill \cr 1 \le b \hfill \cr 0 \le c \le d - 1 \hfill \cr 1 \le d \le b + c \hfill \cr} \right. \quad \Rightarrow \quad \left\{ \matrix{ 0 \le c \le d - 1 \hfill \cr d + e = b + c \hfill \cr 0 \le e \le m - d \hfill \cr a = m - \left( {d + e} \right) \hfill \cr} \right. $$

Then the solution is (almost) right at hand.

We start from (4) and insert the conditions just stated $$ \bbox[lightyellow] { \begin{array}{l} \left( {1 + x + \cdots + x^{u - 1} + x^{\,u} + x^{\,u + 1} + \cdots + x^{\,u + \left( {r - u} \right)} } \right)^m = \\ = \sum\limits_{\left\{ {\begin{array}{*{20}c} {0\, \le \,a,b,c} \\ {a + b + c\, = \,m} \\\end{array}} \right.} {\left( \begin{array}{c} m \\ a,b,c \\ \end{array} \right) \left( {\frac{{1 - x^{\,u} }}{{1 - x}}} \right)^{\;a} x^{\,b\,u} \left( {x^{\,u + 1} \frac{{1 - x^{\,r - u} }}{{1 - x}}} \right)^{\,c} } \\ \quad \quad \quad \quad \Downarrow \\ \sum\limits_{\left\{ {\begin{array}{*{20}c} {0\, \le \,a,e,c} \\ {a + e\, = \,m - d} \\ {0 \le c \le d - 1} \\\end{array}} \right.} {\left( \begin{array}{c} m \\ d + e \\ \end{array} \right) \left( \begin{array}{c} d + e \\ c \\ \end{array} \right) \left( {\frac{{1 - x^{\,u} }}{{1 - x}}} \right)^{\;a} x^{\,e\,u} \; \underbrace {\;x^{\,d\,u} \left( {x\frac{{1 - x^{\,r - u} }}{{1 - x}}} \right)^{\,c} }_{deleted\;part}} = \\ \sum\limits_{\left\{ {\begin{array}{*{20}c} {0\, \le \,e\,\,\left( { \le \,m - d} \right)} \\ {0 \le c \le d - 1} \\\end{array}} \right.} {\left( \begin{array}{c} m \\ d + e \\ \end{array} \right) \left( \begin{array}{c} d + e \\ c \\ \end{array} \right) \left( {\frac{{1 - x^{\,u} }}{{1 - x}}} \right)^{\;m - d - e} x^{\,e\,u} \; \underbrace {\;x^{\,d\,u} x^{\,c} F_{b * } \left( {x,r - u - 1,c} \right)}_{deleted\;part}} \\ \end{array} \tag{5.a}}$$ a comparison of a histogram wrt a version of the same arranged in a non-decreasing order will give a visual grasp on the above.

Now we need to keep the total number of histograms while cancelling the contribution to the exponent of $x$ of the part to be deleted: we can do that by putting $x=1$ in the concerned section
(in the expanded form of $F_{b*}$ or as a limit in the rational form) $$ \bbox[lightyellow] { \begin{array}{l} F_{r * } (x,r,m,d,u)\quad \left| \begin{array}{l} \;1 \le d \le m \\ \;0 \le u \le r \\ \end{array} \right.\quad = \\ = \sum\limits_{\left\{ {\begin{array}{*{20}c} {0\, \le \,e\,\,\left( { \le \,m - d} \right)} \\ {0 \le c \le d - 1} \\\end{array}} \right.} {\left( \begin{array}{c} m \\ d + e \\ \end{array} \right)\left( \begin{array}{c} d + e \\ c \\ \end{array} \right) \left( {\frac{{1 - x^{\,u} }}{{1 - x}}} \right)^{\;m - d - e} x^{\,e\,u} \;F_{b * } \left( {1,r - u - 1,c} \right)} = \\ = \sum\limits_{0\, \le \,e\,\,\left( { \le \,m - d} \right)} {\left( {\sum\limits_{0\, \le \,c\, \le \,d - 1} {\left( \begin{array}{c} d + e \\ c \\ \end{array} \right)\;F_{b * } \left( {1,r - u - 1,c} \right)} } \right) \left( \begin{array}{c} m \\ d + e \\ \end{array} \right)x^{\,e\,u} F_{b * } \left( {x,u - 1,m - d - e} \right)} = \\ = \sum\limits_{0\, \le \,e\,\,\left( { \le \,m - d} \right)} {\left( {\sum\limits_{0\, \le \,c\, \le \,d - 1} {\left( \begin{array}{c} d + e \\ c \\ \end{array} \right)\; \left( {r - u} \right)^c } } \right)\left( \begin{array}{c} m \\ d + e \\ \end{array} \right)x^{\,e\,u} F_{b * } \left( {x,u - 1,m - d - e} \right)} \\ \end{array} \tag{5.b}}$$ and finally $$ \bbox[lightyellow] { \eqalign{ & F_{r * } (x,r,m,d)\quad \left| \matrix{ \;1 \le d \le m \hfill \cr \;0 \le r \hfill \cr} \right.\quad = \cr & = \sum\limits_{0\, \le \,u\,\, \le \,r} {F_{r * } (x,r,m,d,u)} = \cr & = \sum\limits_{0\, \le \,u\,\, \le \,r} {\sum\limits_{0\, \le \,e\,\,\left( { \le \,m - d} \right)} {\left( {\sum\limits_{0\, \le \,c\, \le \,d - 1} {\left( \matrix{ d + e \cr c \cr} \right)\;\left( {r - u} \right)^c } } \right)\left( \matrix{ m \cr d + e \cr} \right)x^{\,e\,u} F_{b * } \left( {x,u - 1,m - d - e} \right)} } \cr} \tag{5.c}}$$

The two formulas above check vs direct computation for low values of the parameters, giving for example

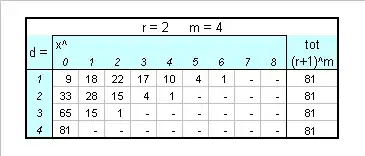
If the deletion concerns lower-filled bins instead, a tweak of the above procedure is quite immediate,
as immediate is the extraction of the coefficients in terms of $N_{b*}$.

6. extension to general multinomial

Concerning your final question, instead of $$ {1 \over {\left( {r + 1} \right)^m }}F_{b * } (x,r,m) = {1 \over {\left( {r + 1} \right)^m }}\left( {1 + x + x^{\,2} + \cdots + x^{\,r} } \right)^m $$ we have $$ G(x,r,m,{\bf p}_r ) = \left( {p_{\,0} + p_{\,1} x + p_{\,2} x^{\,2} + \cdots + p_{\,r} x^{\,r} } \right)^m $$ where ${\bf p}_r$ is a vector of dimension same as $r$

Then the starting of (5.a) will be $$ \begin{array}{l} G(x,r,m,{\bf p}_r ) = \left( {p_{\,0} + p_{\,1} x + p_{\,2} x^{\,2} + \cdots + p_{\,r} x^{\,r} } \right)^m \\ \left( {p_{\,0} + p_{\,1} x + \cdots + p_{\,u - 1} x^{u - 1} + p_{\,u} x^{\,u} + p_{\,u + 1} x^{\,u + 1} + \cdots + p_{\,r} x^{\,u + \left( {r - u} \right)} } \right)^m = \\ = \sum\limits_{\left\{ {\begin{array}{*{20}c} {0\, \le \,a,b,c} \\ {a + b + c\, = \,m} \\\end{array}} \right.} {\left( \begin{array}{c} m \\ a,b,c \\ \end{array} \right) G(x,u - 1,a,{\bf p}_{u - 1} )p_{\,u} ^b x^{\,b\,u} x^{\,\left( {u + 1} \right)\,c} G(x,r - u - 1,c,{\bf \tilde p}_{r - u - 1} )} \\ \end{array} $$ where $\bf \tilde p$ indicates the queue of the vector.

The rest of the procedure is the same and leads to $$ \bbox[lightyellow] { \eqalign{ & G(x,r,m,{\bf p}_r ,d)\quad \left| \matrix{ \;1 \le d \le m \hfill \cr \;0 \le r \hfill \cr} \right.\quad = \cr & = \sum\limits_{0\, \le \,u\,\, \le \,r} {\sum\limits_{0\, \le \,e\,\,\left( { \le \,m - d} \right)} {\left( {\sum\limits_{0\, \le \,c\, \le \,d - 1} {\left( \matrix{ d + e \cr c \cr} \right) \;p_{\,u} ^{d - c} G(x,r - u - 1,c,{\bf \tilde p}_{r - u - 1} )} } \right) \left( \matrix{ m \cr d + e \cr} \right)p_{\,u} ^e x^{\,e\,u} G(x,u - 1,m - d - e,{\bf p}_{u - 1} )} } \cr} \tag{6}}$$

Answer 2

This is simply a naive generalization of whuber's approach. I'm skeptical about whether there will be anything better as far as exact answers go. Certainly there are asymptotics in various regimes, e.g. whuber already noted a Central Limit Theorem experimentally.

For simplicity, consider dropping $2$ out of $n$ $d$-sided dice. Let $f_{n, d, k_1, k_2}(x)$ be the ordinary generating function for the sum of $n$ dice where the smallest is at least $k_1$ and the second-smallest is as least $k_2$. Then $$f_{n, d, k_1, k_2}(x) = (x^{k_1} + x^{k_1+1} + \cdots + x^d)(x^{k_2} + \cdots + x^d)^{n-1} = x^{k_1 + (n-1)k_2} \left(\frac{1-x^{d-k_1+1}}{1-x}\right) \left(\frac{1-x^{d-k_2+1}}{1-x}\right)^{n-1}$$

We want the OGF for the sum of the $n-2$ largest dice where the smallest is exactly $k_1$ and the second-smallest is exactly $k_2$. Well, that's just $$g_{n,d,k_1,k_2}(x) = x^{-k_1-k_2} \begin{cases} f_{n, d, k, k}(x) - f_{n, d, k+1,k+1}(x) & \text{if }k_1 = k_2 = k \\ f_{n, d, k_1, k_2}(x) - f_{n, d, k_1+1, k_2} - f_{n, d, k_1, k_2+1}(x) & \text{if }k_1 < k_2 \end{cases}$$

So, your probability generating function is $$\frac{1}{n^d}\sum_{1 \leq k_1 \leq k_2 \leq d} g_{n, d, k_1, k_2}(x).$$

Clearly this generalizes to dropping $m$ of the dice. The final sum will have $O(d^m)$ terms, so it scales exponentially in $d$.

Answer 3

Here we look somewhat closer at whuber's approach in the line of @JoshuaPSwanson. We identify some subtleties and derive an explicit expression (no recursion) of a generating function giving the sum of $n$ $d$-sided dice when dropping the two smallest values (the case $M=2$).

At first we start with calculating a generating function $G_{n,d,M}(x)$ with small parameters $n=3, d=4$ and $M=2$ to better see what's going on and for plausibility checks.

Example: $n=3,d=4,M=2$

We obtain \begin{align*} \color{blue}{G_{3,4,2}(x)}&=\sum_{1\leq k_1=k_2=k_3\leq 4}\frac{3!}{3!}x^{k_3} +\sum_{1\leq k_1<k_2=k_3\leq 4}\frac{3!}{1!2!}x^{k_3}\\ &\qquad+\sum_{1\leq k_1=k_2\leq k_3\leq 4}\frac{3!}{2!1!}x^{k_3} +\sum_{1\leq k_1<k_2<k_3\leq 4}\frac{3!}{1!1!1}+x^{k_3}\tag{1}\\ &=\sum_{k_3=1}^4x^{k_3}+3\sum_{k_3=2}^4(k_3-1)x^{k_3}+3\sum_{k_3=2}^4(k_3-1)x^{k_3}\\ &\qquad+6\sum_{k_3=3}^4\binom{k_3-1}{2}x^{k_3}\\ &=(x+x^2+x^3+x^4)+3(x^2+2x^3+3x^4)+3(x^2+2x^3+3x^4)\\ &\qquad +6(x^3+3x^4)\\ &\,\,\color{blue}{=x+7x^2+19x^3+37x^4} \end{align*}

We see in (1) the values $1\leq k_1\leq \cdots\leq k_n\leq d$ of the $n$ dice are organised according to $n-1$ operators between consecutive values. These operators are either $<$ or $=$, resulting in $2^{n-1}$ sums. The denominators of the multinomial coefficients reflect the groups of equal values $k_j$. This example was easy to calculate, but since the number of sums increase exponentially, this representation is not useful for large values of $n$.

In order to derive a generating function $G_{n,d,M}(x)$ we look at the building blocks below.

At least and exact information : $f_{n,d,k_1,k_2}(x), g_{n,d,k_1,k_2}(x)$.

We use the same notation as @JoshuaPSwanson and denote with

• $f_{n,d,k_1,k_2}(x)$: The generating function of $n$ $d$-sided dice having smallest value at least $k_1$ and second smallest values at least $k_2$.

• $g_{n,d,k_1,k_2}(x)$: The generating function of $n$ $d$-sided dice having smallest value exactly $k_1$ and second smallest value exactly $k_2$. Additionally $k_1$ and $k_2$ are dropped.

We have for $1\leq k_1\leq k_2\leq d$ the relationship: \begin{align*} f_{n,d,k_1,k_2}(x)=\sum_{{k_1\leq s\leq t\leq d}\atop{k_2\leq t}}x^{-s-t}g_{n,d,s,t}(x)\tag{2} \end{align*}

Inverting relation (2):

It was easy to express $f_{n,d,k_1,k_2}(x)$ as sum of functions $g_{n,d,s,t}(x)$. We can also revert (2) and express $g_{n,d,k_1,k_2}(x)$ as sum of $f_{n,d,s,t}(x)$. In fact the indices $(k_1,k_2)$ carry a partial order of the following form, here shown for the reference example (1).

\begin{align*} \begin{matrix} &&&(k_1,k_2)\\ \\ (1,1)&\rightarrow&\color{blue}{(1,2)}&\color{blue}{\rightarrow}&\color{red}{(1,3)}&\rightarrow&(1,4)\\ &&\color{blue}{\downarrow}&&\color{blue}{\downarrow}&&\downarrow\\ &&\color{red}{(2,2)}&\color{blue}{\rightarrow}&\color{red}{(2,3)}&\rightarrow&(2,4)\\ &&&&\downarrow&&\downarrow\\ &&&&(3,3)&\rightarrow&(3,4)\\ &&&&&&\downarrow\\ &&&&&&(4,4) \end{matrix} \end{align*}

We see in the diagram above when looking for instance at the pair $(k_i,k_j)=(1,2)$ that \begin{align*} x^{1+2}g_{3,4,1,2}(x)=f_{3,4,1,2}(x)-f_{3,4,1,3}(x)-f_{3,4,2,2}(x)+f_{3,4,2,3}(x) \end{align*}

Note that due to subtracting $f_{3,4,1,3}(x)$ and $f_{3,4,2,2}(x)$ the part covered by $f_{3,4,2,3}(x)$ is subtracted twice and we have to compensate it by adding $f_{3,4,2,3}(x)$. This is in fact a consequence of the principle of inclusion-exclusion which comes typically into play when transforming at least information into exact information (see e.g. this answer).

In general we have: \begin{align*} x^{2k}g_{n,d,k,k}(x)&=f_{n,d,k,k}(x)-f_{n,d,k,k+1}(x)\qquad\qquad\qquad\qquad 1\leq k<n\\ x^{k_1+k_2}g_{n,d,k_1,k_2}(x)&=f_{n,d,k_1,k_2}(x)-f_{n,d,k_1+1,k_2}(x)-f_{n,d,k_1,k_2+1}(x)\\ &\qquad+f_{n,d,k_1+1,k_2+1}(x)\qquad\qquad\qquad\qquad\qquad 1\leq k_1<k_2<n\\ x^{k+n}g_{n,d,k,n}(x)&=f_{n,d,k,n}(x)-f_{n,d,k+1,n}(x)\qquad\qquad\qquad\qquad 1\leq k<n\\ x^{2n}g_{n,d,n,n}(x)&=f_{n,d,n,n}(x)\\ \end{align*}

Calculation of $f_{3,4,3,4}(x)$:

Now we are going to evaluate $f_{n,d,k_1,k_2}$. We start with the example (1) and consider the pair $(k_1,k_2)=(3,4)$. Following the answer of @JoshuaPSwanson we obtain \begin{align*} f_{3,4,3,4}(x)\stackrel{?}{=}\left(x^3+x^4\right)\left(x^4\right)^2=x^{11}+x^{12} \end{align*} In fact we instead have according to (2): \begin{align*} f_{3,4,3,4}(x)&=x^{3+4}g_{3,4,3,4}(x)+x^{4+4}g_{3,4,4,4}(x)\\ &=x^{3+4}\left(3x^4\right)+x^{4+4}\left(x^4\right)\\ &=\color{blue}{3}x^{11}+x^{12} \end{align*} The blue marked coefficient $3$ respects the three valid outcomes $\{(3,4,4),(4,3,4),(4,4,3)\}$. In order to derive a generating function for $f_{3,4,3,4}(x)$ we start with $(ax^3+bx^4)^3$ which additionally marks the variables corresponding to $k_1=3$ and $k_2=4$ and use the coefficient of operator $[z^n]$ denoting the coefficient of $z^n$ in a series to filter the wanted parts of the expression.

We calculate \begin{align*} f_{3,4,3,4}(x)&=\left([ab^2]+[b^3]\right)\left(ax^3+bx^4\right)^3\\ &=\left([ab^2]+[b^3]\right)\left(a^3x^9+3a^2bx^{10}+3ab^2x^{11}+b^3x^{12}\right)\\ &=\color{blue}{3}x^{11}+x^{12} \end{align*} and get this way also the wanted coefficients.

Calculation of $f_{n,d,k_1,k_2}(x)$:

In order to find a generating function for $f_{n,d,k_1,k_2}(x)$ we use formula (2) above and calculate $g_{n,d,s,t}(x)$. We obtain for $1\leq s<t\leq d$: \begin{align*} \color{blue}{x^{s+t}}&\color{blue}{g_{n,d,s,t}(x)}\\ &=\left([ab]+[ab^2]+\cdots+[ab^{n-1}]\right)\left(ax^s+bx^t+x^{t+1}+\cdot+x^d\right)^n\tag{3}\\ &=\left([ab]+\cdots+[ab^{n-1}]\right)\sum_{j=0}^n\binom{n}{j}a^jx^{sj}\left(bx^t+x^{t+1}+\cdots+x^d\right)^{n-j}\\ &=\left([b]+\cdots+[b^{n-1}]\right)\binom{n}{1}x^{s}\left(bx^t+x^{t+1}+\cdots+x^d\right)^{n-1}\tag{4}\\ &=nx^s\left([b]+\cdots+[b^{n-1}]\right)\binom{n}{1}\sum_{j=0}^{n-1}\binom{n-1}{j}b^jx^{tj}\left(x^{t+1}+\cdots+x^d\right)^{n-1-j}\\ &=nx^s\sum_{j=1}^{n-1}\binom{n-1}{j}x^{tj}\left(x^{t+1}+\cdots+x^d\right)^{n-1-j}\tag{5}\\ &=nx^s\left(\left(x^t+\cdots+x^d\right)^{n-1}-\left(x^{t+1}+\cdots+x^d\right)^{n-1}\right)\\ &\,\,\color{blue}{=nx^s\left(\frac{x^t-x^{d+1}}{1-x}\right)^{n-1}-nx^s\left(\frac{x^{t+1}-x^{d+1}}{1-x}\right)^{n-1}}\tag{6} \end{align*}

Comment:

• In (3) we have to assure that $k_1=s$ occurs exactly once. So, we have to select $[a]$ and no other powers of $a$. We also have to assure that $k_2=t$, but more occurrences of $t$ are allowed, so we have to select $[b]+[b^2]+\cdots+[b^{n-1}]$.

• In (4) we select the coefficient of $a$.

• In (5) we select the coefficients of $b^j$.

In a similar way we obtain for $1\leq s=t\leq d$: \begin{align*} x^{2t}g_{n,d,t,t}(x)&=\left([a^2]+\cdots+[a^n]\right)\left(ax^t+x^{t+1}+\cdots+x^d\right)^n\\ &=\left(\frac{x^t-x^{d+1}}{1-x}\right)^{n}-\left(\frac{x^{t+1}-x^{d+1}}{1-x}\right)^{n}\\ &\qquad-nx^t\left(\frac{x^{t+1}-x^{d+1}}{1-x}\right)^{n-1}\tag{7} \end{align*}

Calculation of $G_{n,d,2}(x)$:

With (2) and the intermediate results (6) and (7) we finally obtain \begin{align*} \color{blue}{G_{n,d,2}(x)}&=\sum_{1\leq s\leq t\leq d}g_{n,d,s,t}(x)\\ &=\sum_{1\leq s=t\leq d}g_{n,d,t,t}(x)+\sum_{1\leq s<t\leq d}g_{n,d,s,t}(x)\\ &=\sum_{t=1}^d\left(x^{-2t}\left(\frac{x^t-x^{d+1}}{1-x}\right)^n-x^{-2t}\left(\frac{x^{t+1}-x^{d+1}}{1-x}\right)^n\right.\\ &\qquad\qquad\left.-nx^{-t}\left(\frac{x^{t+1}-x^{d+1}}{1-x}\right)^{n-1}\right)\\ &\qquad +n\sum_{t=2}^d(t-1)x^{-t}\left(\left(\frac{x^t-x^{d+1}}{1-x}\right)^{n-1}-\left(\frac{x^{t+1}-x^{d+1}}{1-x}\right)^{n-1}\right)\\ &=\cdots\\ &=x^{-2}\left(\frac{x-x^{d+1}}{1-x}\right)^{n}+\left(1-x^2\right)\sum_{t=2}^dx^{-2t}\left(\frac{x^t-x^{d+1}}{1-x}\right)^{n}\\ &\qquad+n(1-x)\sum_{t=2}^{d}(t-1)x^{-t}\left(\frac{x^t-x^{d+1}}{1-x}\right)^{n-1}\\ &\,\,\color{blue}{=x^{n-2}\left(\frac{1-x^{d}}{1-x}\right)^{n}+\left(1-x^2\right)\sum_{t=1}^dx^{(n-2)t}\left(\frac{1-x^{d-t+1}}{1-x}\right)^{n}}\\ &\qquad\color{blue}{+n(1-x)\sum_{t=1}^{d}(t-1)x^{(n-2)t}\left(\frac{1-x^{d-t+1}}{1-x}\right)^{n-1}}\tag{8}\\ \end{align*}

Plausibility check:

We obtain from (8): \begin{align*} \color{blue}{G_{3,4,2}(x)}&=x^3\left(1+x+x^2+x^3\right)^3 +\left(1-x^2\right)\sum_{t=1}^4x^t\left(1+\cdots+x^{4-t}\right)^3\\ &\qquad+3(1-x)\sum_{t=1}^4(t-1)x^t\left(1+\cdots+x^{4-t}\right)^2\\ &=x^3+3x^4+6x^5+10x^6+12x^7+12x^8+10x^9+6x^{10}+3x^{11}+x^{12}\\ &\qquad+\left(x+4x^2+9x^3+16x^4+12x^5-x^6-9x^7\right.\\ &\qquad\qquad\qquad\left.-12x^8-10x^9-6x^{10}-3x^{11}-x^{12}\right)\\ &\qquad+3\left(x^2+3x^3+6x^4+6x^5-6x^6-6x^7-3x^8-x^9\right)\\ &\,\,\color{blue}{=x+7x^2+19x^3+37x^4} \end{align*} in accordance with (1).

Note, that whuber's formula (4) when multiplied with $d^n$ can be written as

\begin{align*} G_{n,d,1}(x)=x^{n-1}\left(\frac{1-x^{d-t+1}}{1-x}\right)^{n} +(1-x)\sum_{t=2}^{d}x^{(n-1)t}\left(\frac{1-x^{d-t+1}}{1-x}\right)^{n} \end{align*} showing the structural similarity with (8).