5

Let's say there is a real-valued "signal" that you can only measure at discrete points $f(x)$. You have a theory that this signal is the result of an analytic function $f(z)$ on the complex plane but, again, you can only measure this function on the real number line.

For example, the signal might look like the picture on the left, while the actual function on the complex plane is on the right (a simple pole at $1\pm1/2i$):

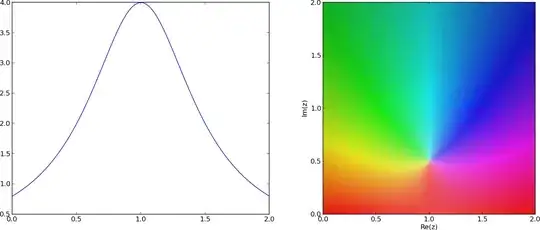
enter image description here

The function could be more complicated, but let's posit that the function only contains complex conjugate zeros, e.g.

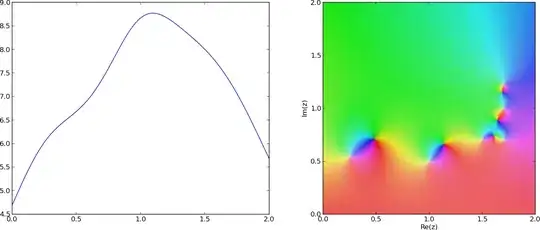
enter image description here

This is a academic question, related to physics (c.f. my answer on “The Egg:” Bizarre behavior of the roots of a family of polynomials for more information on the context), but I'm looking for mathematical insight.

The zeros of $f(z)$ are important because they impart asymptotics onto the measurable $f(x)$, roughly the further away the zero is from the real number line, the "less important" it is to the function.

Question: Given only $f(x)$ and the assumption that it is analytic on the complex plane with only a finite set of simple complex conjugate poles, what can we say about the zeros on the complex plane?

Community
  • 1
Hooked
  • 6,637
  • 2
    Virtually nothing. If $p$ is a polynomial with the pole places as roots (with appropriate multiplicity) and $g$ is entire, then $f(z)=\frac{g(z)}{p(z)}$ has your prescribed poles, but quite arbitrary zeroes. ($g$ could be an arbitrary polynomial, the exponential, $(z-1)\zeta(z)$ or whatever) – Hagen von Eitzen Apr 29 '13 at 16:26
  • @HagenvonEitzen: I was about to write more or less the same comment, but I think the question might be something like given the values of $f$ on the real line, and the restriction that $f$ is rational with conjugate poles, then what can you say about the zeros of $f$? – copper.hat Apr 29 '13 at 16:45
  • @HagenvonEitzen even if you can't say much about the zeros of $f$, what about the zeros of $f'$? I ask because it looks like the peaks of $f$ on the trivial examples I gave above correspond to the poles, with the "spread" related to their proximity to the real number line. – Hooked Apr 29 '13 at 17:26

0 Answers0