Geometrical interpretation of $\frac{\sin(\alpha)}{\alpha}$

Question

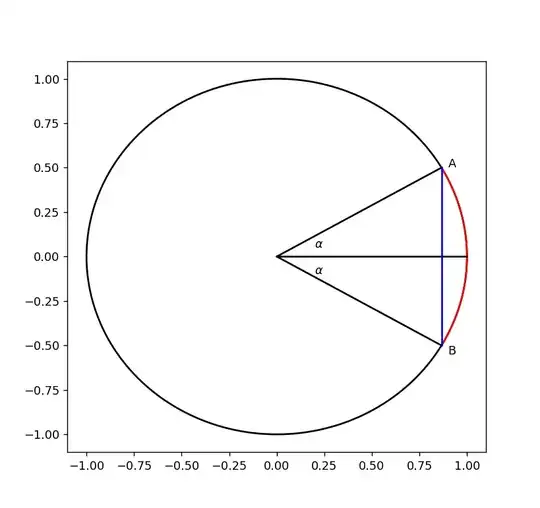
What is the geometrical interpretation of this quantity $$\frac{\sin(\alpha)}{\alpha}$$ such that $\alpha\in(0,\pi/2)$

For example, this is the abscissa of the centroid of the arcs of the unit circle centered at the origin of angle $2\alpha$ and symmetric with respect to the axis of abscissa.

Is there any other geometrical interpretation of this quantity or can we characterize this centroid by another method

You may take $\alpha$ as an arc length corresponding to an angle $\alpha$ of a unit circle. — VIVID, Jul 18 '20 at 17:40
https://math.stackexchange.com/questions/75130/how-to-prove-that-lim-limits-x-to0-frac-sin-xx-1 — Khosrotash, Jul 18 '20 at 17:48
Some of proof are there by geometric concept...take a look ,maybe help you — Khosrotash, Jul 18 '20 at 17:53
Note that $\sin(\alpha)/\alpha$ is also called the unnormalized sinc function. — None, Jul 18 '20 at 19:26
@Bernstein: I do not think there is restriction for $\alpha\in(0,\pi/2)$ — Narasimham, Jul 18 '20 at 19:48
Please do not use inappropriate tags. Nothing here with linear algebra or differential geometry. — Ted Shifrin, Jul 18 '20 at 22:26
@TedShifrin thanks for your remark, I have read your courses on Diff Geo it was very nice for me. many thanks with a lot of admiration :) — Bernstein, Jul 19 '20 at 11:11

Andrei · Accepted Answer · 2020-07-18T23:01:19.593

5

Based on the previous hints, in a circle of radius $R$, take lines from the center, forming an angle $2\alpha$. The lines intersect the circle at $A$ and $B$. Then the length of the arc between them is $2R\alpha$, and the length of the chord is $2R\sin\alpha$. So $$\frac{\sin\alpha}{\alpha}=\frac{|\overparen{AB}|}{|AB|}$$ is the ratio of the cord length to the arc length for two points on the circle, forming an angle $2\alpha$ from the origin. ** As requested** I've added an image. The ratio is the length of the blue line to the length of the red arc.

edited Jul 18 '20 at 23:01

answered Jul 18 '20 at 22:20

Andrei

37,370

I think you need put picture – tryst with freedom Jul 18 '20 at 22:26
@DDD4C4U I've modified my answer as requested – Andrei Jul 18 '20 at 23:01

score 0 · Answer 2 · answered Jul 19 '20 at 07:51

When we consider one half of the arc only:

$$ \bar{x}= \dfrac{\int x ds}{\int ds} = \dfrac{\int x ds}{\int ds} $$ with $ s = R \theta,\,$ the centroid $x$ location is

$$ \dfrac{\int_0^\alpha R \cos \theta R d\theta}{\int _0^\alpha R d\theta} =R\dfrac{\sin \alpha}{\alpha}$$

similarly for $ y= R \cos \theta $

$$ \bar{y}=R\dfrac{\;1-\cos \alpha}{\alpha}$$

Centroid locus for a half one side extending arc is shown.

So $\alpha $ need not be bounded.

$$ \alpha\rightarrow \infty, \bar{r} \rightarrow 0$$

Geometrical interpretation of $\frac{\sin(\alpha)}{\alpha}$

2 Answers2