Although I'm posting this an an answer, it's more of a continuation and clarification of the comments I added earlier. Regardless, I will attempt to aid in a solution to the "paradox". I hope you enjoy or find some of the following as fascinating as I do.
This question is actually really ellegant as it delves into the nature of infinity. I'm sure anyone invested in mathematics has heard something like the phrase "some infinities are larger than others". This eludes to there being a great variety in different types of infinities. Despite there being many types, often we simply use the symbol $\infty$ to denote all of them.
This works for most scenarios, like most of calculus. However, even a new undergrad will quickly be introduced to the difference between "countable" and "uncountable" infinities.
Ordinals & cardinals
Before I touch on infinity, I'd like to introduce the concepts of "ordinal numbers", and "cardinal numbers".
In brief, most numbers we're familiar with can be used with different intention to be either an ordinal or cardinal. When we're using numbers to represent size/magnitude/amounts of something, we're dealing with cardinals. But when we're using numbers to represent an index/placement, we're dealing with ordinals.
For example, the amount of apples in your box $S$, is a cardinal. Meanwhile the apple at index $N$, is an ordinal. Hence, there could be a time where $S=5$ and another when $N=5$, but in one case 5 is a cardinal and in the other 5 is an ordinal.
Infinite ordinals
Since ordinals deal intrinsically with placement/order, if you were to label an "infinite" number of apples, there's nothing stopping you from labeling one more. Let me introduce $\omega$, the smallest ordinal infinity.
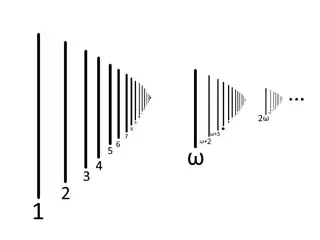
In this diagram each line is labelled with it's corresponding ordinal. Notice how once we've labelled the lines using all the natural numbers $1,2,3\rightarrow\dots$, we can start labeling a second batch of infinite lines starting with $\omega, \omega+1,\omega+2\rightarrow\dots$.
Side note: In this context, that plus sign in $\omega+1$ doesn't exactly mean we're adding 1 to $\omega$, it might be better to say we're simply referring to the ordinal that is directly after $\omega$.
Anyways, after that second batch can start our third batch with $2\omega$ and so on. As you can see, we can proceed to label an infinite amount of infinitely-sized batches. Here is one of my favorite diagrams depicting the same line labeling game spiraling towards $\omega^\omega$
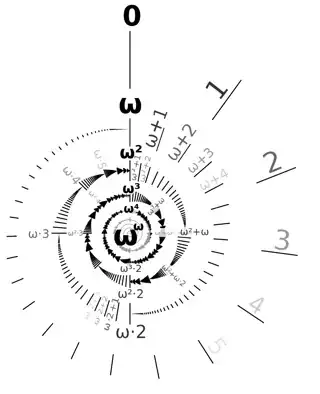
But it does not stop there! You could continue the labeling game to $\omega^{\omega^\omega}$ then $\omega^{\omega^{\omega^\omega}}$, and so on. Current mathematics literally has no limit to the size of ordinal infinities. In fact, we've tried several times to define the "largest possible ordinal" and nearly every time another mathematician comes along and defines a larger one. See Large countable ordinal on Wikipedia for some of these attempts.
Infinite cardinals
Slowly looping back to your question, let's go back to a more familiar type of infinity. Mathematician's use the symbol $ℵ_0$ to denote the cardinality of the set of natural numbers. I.e; the type of infinite to represent the amount of numbers in a countable set. It is the smallest cardinal infinity.
This type of infinity may be seen as more intuitive, as $ℵ_0+1=ℵ_0$. Even though adding a finite number to $ℵ_0$ doesn't change it's value, there are still bigger infinities. For example, the cardinality of the set of real numbers is $2^{ℵ_0}$, often denoted in some theories as $$ or $ℵ_1$. See Aleph numbers and Cardinality of the continuum.
Back to your question
To reiterate your question, we start with an apple with ordinality one and an box with cardinality zero. At step $n$ ($n$ is an ordinal!), we put apples $2n-1$ and $2n$ into the box, then take apple $n$ out. With each step, the carnality of the box goes up by 1.
Let's say we now go through an "infinite" number of steps. That really doesn't mean anything unless you specify which infinity.
Solving the paradox
Suppose we stop after $\omega$ steps, the smallest ordinal infinity. At step $\omega$, we've taken out all apples labelled $\omega$ or less. However we have now just put in apples labelled $2\omega-1$ and $2\omega$. Thus within the box there are still apples apples labelled $\omega+1$ through $2\omega$. Therefore the cardinality (amount) of apples in the box is $S=ℵ_0$. This is intuitive as despite removing an infinite number of apples, there's an equal amount still in the box. No paradox here!
But indeed, could a paradox arise after more than $\omega$ steps? That's where it gets a little more confusing. This MathSE question shows that no matter what step $n$ we stop at, since $n$ is a countable ordinal (because we're counting apples), the amount of apples in the box is still $ℵ_0$. Therefore, for a paradox to arise, we'd have to label apples beyond all countable ordinals, which is not even close to being a comprehensible idea. What would it mean to label apples so far beyond infinity, that we've run out of infinities?
From what I understand (and that's very little), it is not possible to "run out" of ordinals, especially in this very linear step-by-step process. What this means is that if we stop at any countable point after $\omega$ steps, there will always be $ℵ_0$ apples in the box. Attempting to wrap my head around going beyond countable ordinals, it could be possible to have more than $ℵ_0$ apples in the box (which wouldn't be paradoxical), but I'm probably already far beyond the scope of this question (let alone my understanding).
The paradox returns
All that said, if I recall correctly from a VSauce video How To Count Past Infinity on the subject (highly recommended), there is a number denoted $\Theta$ (possibly this number), which describes an ordinal so incredibly beyond $\omega$ and $\omega^{\omega^{\omega^\omega}}$, etc, that it is not possible to be reached with current methods of transfinite labeling.
If it's possible to even conceive of $\Theta$ steps, then it is possible for a paradox to arrive where you've exhausted all countable ordinals. In that case the number of apples left in the box may indeed be zero. If true, then such paradox only arrived because we pushed the bounds of infinity to it's breaking point. Here, mathematics dissolves. The nature of this type of infinity does what it pleases.
Concluding remarks
In conclusion, as far as mathematics is concerned, there's no paradox; the logic works out. Though as math is built on logic, going beyond the infinities that math can handle, logic no longer applies.

