This operation seems to have nothing to do with any of the usual meanings of reflection. As an example, this operation is not an involution. (This operation produces (some) points in the interior of the convex set bounded by the parabola. No tangent to the parabola contains any point in that interior, so this operation produces points for which this operation is subsequently undefined.)
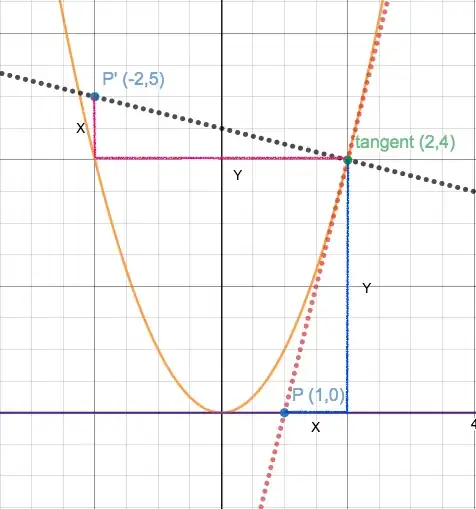
Let's parametrize the parabola as $(t,t^2)$. (So $x =t$, $y = t^2$, and then $y = x^2$.) The slope of the tangent to the parabola at $(t,t^2)$ is $2t$ (by the power rule from calculus). So we seek the intersection of the lines (the tangent here written in point-slope form)
$$ \begin{cases} y-t^2 = 2t(x - t) & \\ y = 0 &\end{cases} $$
Eliminating $y$ and solving for $x$, we find $x = t/2$. (Strictly, we find this for $t \neq 0$ by manipulation of the above, because the division by $2t$ is undefined when $t=0$. But then, when $t =0$, the point on the parabola is its vertex and is a point on the line $y=0$, with $x = 0 = 0/2$, so as a happy coincidence, the same expression is correct even when the division is invalid.)
The distance between $(t,t^2)$ and $(t/2,0)$ is
$$ d = \sqrt{(t-t/2)^2 + (t^2-0)^2} = \sqrt{t^4 + t^2/4} \text{.} $$
Any line perpendicular to the tangent has slope $-1/(2t)$. We seek the intersection of the line perpendicular to the tangent through the point $(t,t^2)$ and the circle centered at $(t,t^2)$ with radius $d$. That is, the solution(s) of
$$ \begin{cases}
y-t^2 = \frac{-1}{2t}(x - t) & \\
(x-t)^2 + (y-t^2)^2 = d^2 = t^4 + \frac{t^2}{4}
\end{cases} \text{.} $$
This line includes a diameter of the circle, so there are two points of intersection (if $d >0$) and we always want the point whose $y$-coordinate is greater than $t^2$ (i.e., the point higher than the point on the parabola).
(If an appeal to diagram is unsatisfying, we can show this as follows: When $t > 0$, the slope of the tangent is $2t>0$, so the slope of the perpendicular is $-1/(2t) < 0$. We keep the point to the left of the point on the parabola, so we ascend the perpendicular to that point. A mirrored argument applies when $t < 0$. When $t = 0$, $d = 0$ and all the points discussed are the origin.)
It is convenient to solve this separately for $t>0$ and $t<0$ (so that we know which of the two roots of a quadratic to keep). We obtain \begin{align*}
(x,y) = \begin{cases}
\left(t+t^2, \frac{1}{2}(2t^2 - t) \right) ,& t < 0 \\
(0,0) ,& t = 0 \\
\left( t - t^2, \frac{1}{2}(2t^2+t) \right) ,& t > 0
\end{cases} \text{.}
\end{align*}
This gives a parametrization of the locus of points described by the operation in the Question. This locus is the union of a semiinfinite segment from each of two rotated parabolas.
We can plot this. The given line and parabola are dashed in blue, the parabolic segment produced by the operation applied to the right half-parabola is in orange and that from the left half is in green.
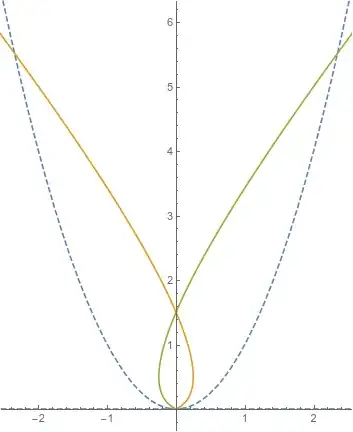
It should perhaps be unsurprising that the locus exits the convex set bounded by the parabola. Parabolas are "taller" than they are "wide" and the tangent constructed in the operation becomes close to vertical as we go to the right or left away from the $y$-axis. So the tangent more and more closely approximates a vertical line, so the distance between the various points is greater than and more closely approximates the "height" of the point on the parabola, which distance will eventually exceed the "width" along the perpendicular (which is increasingly closer to horizontal).
Details of the last computation were requested. Note that $t = 0$ gives $(x,y) = (0,0)$ so that case is automatic. Henceforth, assume $t \neq 0$. From
$$ \begin{cases}
y-t^2 = \frac{-1}{2t}(x - t) & \\
(x-t)^2 + (y-t^2)^2 = d^2 = t^4 + \frac{t^2}{4}
\end{cases} $$
observe the common term $y-t^2$. It appears to the first order alone on the left of the first equation, so we substitute the right of the first equation into the second.
$$ (x-t)^2 + \left( \frac{-1}{2t}(x - t) \right)^2 = t^4 + \frac{t^2}{4} $$
expands to
$$ (x-t)^2 + \frac{1}{4t^2}(x - t)^2 = t^4 + \frac{t^2}{4} \text{.} $$
Clearing denominators (permissible because $4t^2 \neq 0$),
$$ 4 t^2(x-t)^2 + (x - t)^2 = 4 t^2 t^4 + t^2 t^2 \text{,} $$
and factoring (un-distributing on both sides),
$$ (4 t^2 + 1)(x-t)^2 = (4 t^2 + 1)t^4 \text{.} $$
Since $4t^2 + 1$ is never zero for any real $t$, we obtain
$$ (x-t)^2 = t^4 \text{.} $$
Taking square roots,
$$ |x-t| = |t^2| = t^2 \text{,} $$
the last equality because the square of a real number is either zero or positive, so equals its absolute value. This gives two possibilities for $x$:
- $x - t = t^2$, so $x = t+t^2$. Putting that back into the first of the two starting equations,
$$ y - t^2 = \frac{-1}{2t}t^2 \text{,} $$
so
$$ y = t^2 - \frac{1}{2}t = \frac{1}{2}(2t^2 - t) \text{.} $$
- $x - t = -t^2$, so $x = t - t^2$. Putting that back into the first of the two starting equations,
$$ y - t^2 = \frac{1}{2t}t^2 \text{,} $$
so
$$ y = t^2 + \frac{1}{2}t = \frac{1}{2}(2t^2 + t) \text{.} $$
To determine the constraints on $t$ in each piece, notice that in the first equation, $y - t^2 > 0$ because this is always the amount the point on the locus is above the point on the parabola. (Recall that we always ascend the perpendicular to arrive at the point on the locus.) This forces the right-hand side also positive. If $t > 0$, $\frac{-1}{2t}$ is negative, so $x-t$ is negative, so the point of the locus is to the left of the point on the parabola. This only occurs on the right half of the parabola, where $t > 0$, since on that half of the parabola, the perpendicular ascends to the left. Symmetrically, when $t < 0$, $\frac{-1}{2t}$ is positive, the perpendicular ascends to the right and $x-t$ is positive.