2

I want to show that the sum of integer squares from $i=1$ to $n$ is $\frac{n(n+1)(2n+1)}{6}$ I've watched some videos and read other posts about it but haven't been able to find anything that makes it click. I know the rate of the difference of consecutive partial sums for $S(n)$ shows $S$ is a cubic function. I tried making use of this using a system of equations with $S(n)=An^3+Bn^2+Cn+D$ at $n=0, 1, 2, 3$, and I ended up getting $S(n)=-\cfrac{643}{24}n^3-\cfrac{131}{8}n^2+\cfrac{137}{12}n$ but I'm unsure how to factor this

Is there a simple approach to this that doesn't involve some weird collapsing sum?

Lex_i
  • 2,072
  • 10
  • 26
  • 1
    Hello, did you try Induction? – Basel J. Jul 14 '20 at 20:55
  • 2
    Double check your computation, the coefficients seem wrong. –  Jul 14 '20 at 20:56
  • 1
    Use the expansion of $(n+1)^3-n^3$ and telescoping. You'll need Gauss's formula for the sum of the first $n$ positive integers for this route. – Favst Jul 14 '20 at 20:57
  • 1
    As you didn't show your work, we can't tell where you went wrong. You know the factorization-it is in the first line. The expanded version is $\frac{n^3}3+\frac{n^2}2+\frac n6$. Your version goes negative for $n$ not very large. – Ross Millikan Jul 14 '20 at 21:14
  • Not super rigorous, but this amazing animation is a nice visual proof. In fact watch the entire video, it's fantastic. – K.defaoite Jul 14 '20 at 22:47
  • @JamesA Either one is fine, but I prefer derive. – Lex_i Jul 15 '20 at 00:28
  • @K.defaoite I saw a couple animations just like that, they were wonderful and absolutely convinced me of the formula. They're great for visualization but not great for note-taking – Lex_i Jul 15 '20 at 00:33
  • @RossMillikan My mistake was when trying to express as matrices and converting the matrix to row echelon form, i made a series of mistakes from not readjusting previous rows. I just went straight column after column. – Lex_i Jul 15 '20 at 00:34
  • See this question. – Axion004 Jul 17 '20 at 17:23

8 Answers8

4

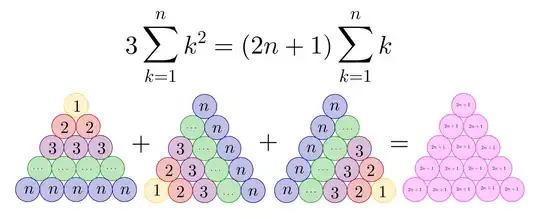
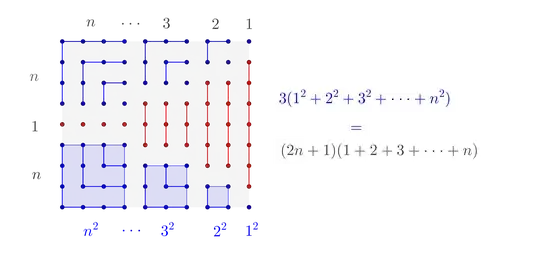
A beautiful proof without words that I recently learned from a friend of mine (credits to KK): enter image description here

Some words of explanation: we have a function $f$ with a constant gradient defined over a domain which is an equilateral triangle. When we consider $g=f+f_{\omega}+f_{\omega^2}$, where $f_\omega$ and $f_{\omega^2}$ are the functions defined over the domain rotated by $120^\circ$ and $240^\circ$, we have that $g$ has a null gradient, hence it is constant.

Jack D'Aurizio
  • 353,855
2

The unique cubic polynomial by the points $(0,0),(1,1),(2,1+4),(3,1+4+9)$ can be obtained as the Lagrangian interpolation polynomial or by indeterminate coefficients, forming the Vandermonde system

$$\begin{pmatrix}0&0&0&1\\1&1&1&1\\8&4&2&1\\27&9&3&1\\\end{pmatrix}\begin{pmatrix}a\\b\\c\\d\\\end{pmatrix}=\begin{pmatrix}0\\1\\5\\14\end{pmatrix}.$$

1

$$An^3+Bn^2+Cn+D-\left(A(n-1)^3+B(n-1)^2+C(n-1)+D\right)\equiv n^2$$ $$3 A n^2 - 3 A n + A + 2 B n - B + C\equiv n^2$$ $$\begin{cases} 3A=1\\-3A+2B=0\\A-B+C=0\\ A+B+C+D=\sum\limits_{k=1}^{1} k^2=1 \end{cases}$$ $$\begin{cases} A=\frac13\\ B=\frac12\\ C=\frac16\\ D=0 \end{cases}$$ $$\frac16\left(2n^3+3n^2+n\right)= \frac16\cdot n\cdot\left(2n^2+3n+1\right)=\frac{n(2n+1)(n+1)}{6}$$

Alexey Burdin
  • 5,214
  • This is an efficient method because it leads to a triangular system of equations. –  Jul 14 '20 at 21:37
0

Observe that

$$4\cdot5\cdot6-0\cdot1\cdot2 \\=(1\cdot2\cdot3+2\cdot3\cdot4+3\cdot4\cdot5+4\cdot5\cdot6)-(0\cdot1\cdot2+1\cdot2\cdot3+2\cdot3\cdot4+3\cdot4\cdot5) \\=3\,(1\cdot2+2\cdot3+3\cdot4+4\cdot5)$$

and more generally

$$(n-1)n(n+1)=3\sum_{i=2}^n (i-1)i=3\sum_{i=1}^n i^2-3\sum_{i=1}^n i.$$

Note that this trick will work for the sums of falling factorials like $(i-k+1)\cdots(i-2)(i-1)i$, and you can establish the relation to the powers $i^k$ via the Stirling numbers of the second kind.

0

I think this is what you tried to do, but you must have made an arithmetic mistake.

$S(0)=0$, $S(1)=1$, $S(2)=5$, and $S(3)=14$. That is,

$D=0\tag1,$ $A+B+C+D=1\tag2,$ $8A+4B+2C+D=5\tag3,$ $27A+9B+3C+D=14\tag4.$

Therefore, $A+B+C=1\tag5,$ $8A+4B+2C=5,\tag6$ $27A+9B+3C=14.\tag7$

Subtracting twice $(5)$ from $(6)$ yields $6A+2B=3\tag8;$ subtracting $3\times(5$) from $(7)$ yields $24A+6B=11\tag9.$

Subtracting $3\times(8)$ from $(9)$ yields $6A=2$ or $A=\frac13$.

Now you should be able to find correct values of $B$ from $(8)$ or $(9)$ and $C$ from $(2)$ or $(3)$ or $(4)$.

J. W. Tanner
  • 60,406
  • Yes that's exactly what I tried to do! I used matrices and tried to rewrite in row echelon form, but looking back I realized i forgot to readjust previous rows – Lex_i Jul 15 '20 at 00:30
0

Sum of squares: The Pythagorean way

enter image description here

Markus Scheuer
  • 108,315
0

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ Note that $\ds{k^{\underline{1}} = k}$ and $\ds{k^{\underline{2}} = k\pars{k -1} = k^{2} - k^{\underline{1}}}$ such that $\ds{k^{2} = k^{\underline{2}} + k^{\underline{1}}}$. Then, \begin{align} \sum_{k = 1}^{n}k^{2} & = \sum_{k = 0}^{n}\pars{k^{\underline{2}} + k^{\underline{1}}} = \pars{{1 \over 3}\,k^{\underline{3}} + {1 \over 2}\,k^{\underline{2}}}_{\ k\ =\ n +1} \\[5mm] & = {1 \over 3}\,\pars{n + 1}^{\,\underline{3}} + {1 \over 2}\,\pars{n + 1}^{\,\underline{2}} \\[5mm] & = {1 \over 3}\pars{n + 1}n\pars{n - 1} + {1 \over 2}\pars{n + 1}n \\[5mm] & = n\pars{n + 1}\bracks{{1 \over 3}\pars{n - 1} + {1 \over 2}} = \bbx{n\pars{n + 1}\pars{2n + 1} \over 6} \end{align}

See Section ${\bf 2.6}$ $\ds{\pars{\bf\mbox{FINITE AND INFINITE CALCULUS}}}$ in Concrete Mathematics by $\mbox{R. L. Graham}$, D. E. Knuth and O. Patashnik, $\ds{2^{\underline{nd}}}$ ed., Addison Wesley Publishing Company.
Felix Marin
  • 89,464
0

You're making this harder than it really is. Note: $$\sum_{k=1}^n k^2=\sum_{k=0}^n (n-k)(2k+1)$$ To visualize this see the squares stacked on top of each other with the largest at the bottom and smallest at the top. Then, first observe that $1$ is in all the squares then there is $(n-0)(1)=n$ in total from $1$. Then, since the next smallest square is $2^2$ it has $2(1)+1$ as a difference of consecutive squares and so will every larger square again yielding $(n-1)(2(1)+1)$ and in general $(n-k)(2k+1)$. Now the algebra, $$(n-k)(2k+1)=2kn+n-2k^2-k=n^3+2n^2+n-2\sum_{k=1}^n k^2-\frac{n(n+1)}{2}$$ which simplifies to $$n^3+n^2+\frac{n(n+1)}{2}=3\sum_{k=1}^n k^2$$ and finally $$\frac{2n^3+3n^2+n}{6}=\frac{n(2n+1)(n+1)}{6}$$

Robotichate
  • 1