Consider the following game: you start with $ n $ coins. You flip all of your coins. Any coins that come up heads you "remove" from the game, while any coins that come up tails you keep in the game. You continue this process until you have removed all coins from the game. Let your score $ s $ be defined as the number of rounds of flipping before the game was over (including the last flip, say).
Let $ a_n $ be the expected value of the score when you start with $ n $ coins. It is not hard to see that $$ a_n = \frac{1}{2^n - 1} \left(1 + \sum_{m=0}^{n-1}{{n\choose m} (a_m + 1)}\right) $$
Are there any generating functionology wizards out there who know if this could be turned into a closed-form formula for $ a_n $?
Note, this question was asked here: You are flipping n fair coins, putting aside those that come up heads after each flip. What's the expected number of rounds?, but the answer is entirely unsatisfactory; they only provide a heuristic which is asymptotically correct.
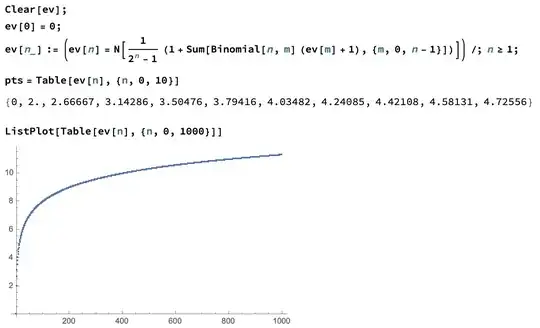
Edit: here is a quick mathematica experiment:
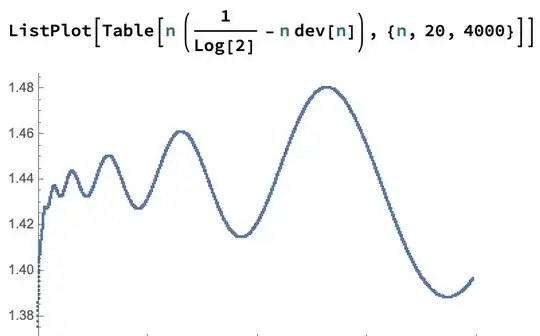
Edit 2: While investigating the first differences of this function, we find a lovely pattern. I plotted the following function $$ g(n) := n \left( \frac{1}{\log(2)} - n (a_{n+1} - a_{n}) \right) $$ resulting in the following plot, clearly oscillating about $ 1/\log(2) $:
(Here, "dev[n]" is the first-difference function $ a_{n+1} - a_n $.)