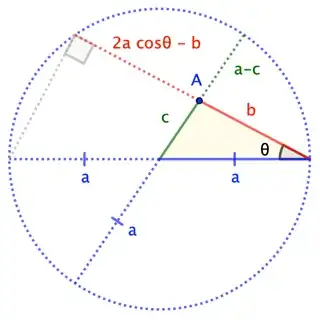
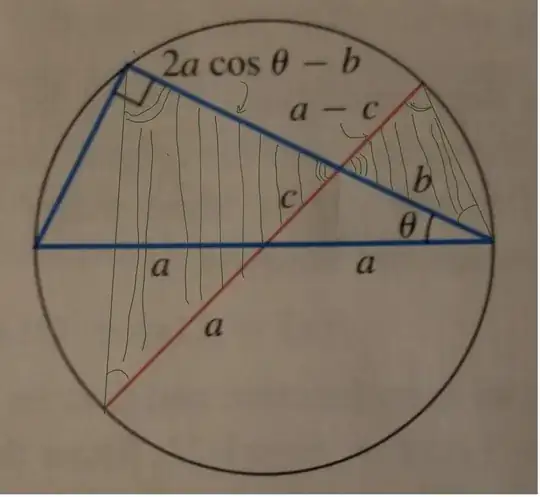
I am trying to prove the Law of Cosines using the following diagram taken from Thomas' Calculus 11th edition.
I have an answer, but I think there must be a simpler or better way to do it. Here is my answer:
Construct a coordinate system such that $(0,0)$ is located at the bottom right corner of the pictured triangle. Then the red line intersects the hypotenuse at $(-a,0)$ and a leg at $(-b\cos\theta,b\sin\theta)$. Thus the squared distance $c$ from $(-a,0)$ to $(-b\cos\theta,b\sin\theta)$ is \begin{align} c^2&=(-b\cos\theta-(-a))^2 + (b\sin\theta)^2\\ &=a^2-2ab\cos\theta+b^2\cos^2\theta+b^2\sin^2\theta\\ &=a^2+b^2-2ab\cos\theta. \end{align}
I feel like there has to be a simpler way, since my proof is basically ignoring the right triangle, the circle, etc. If somebody can show me another proof, that would be great. Thanks.
UPDATE: It looks like I needed the Intersecting Chords Theorem from Geometry to write $(a+c)(a-c)=(2a\cos\theta-b)(b)$.