1

I'm trying to solve this exercise from Ravi Vakil's notes on AG, which is labeled as trivial there but doesn't seem to be as such. It is assumed that both $X_1 \times_Y X_2$ and $X_1 \times_Z X_2$ exist for given maps $\alpha_{1,2}: X_1,X_2 \rightarrow Y$, $\beta_{1,2}:X_1,X_2 \rightarrow Z$. Also label $\pi^Y_{1,2}:X_1 \times_Y X_2 \rightarrow X_1,X_2$, $~\pi^Z_{1,2}:X_1 \times_Z X_2 \rightarrow X_1,X_2$, $~f:Y \rightarrow Z$. Sorry in advance for the absence of a diagram, but I couldn't think of anything other than something like here in the first answer (without the bottom right half) and it seems wrong to me for the reasons I describe below.

My first solution attempt was to notice, that $\alpha_1 \circ \pi^Y_1 = \alpha_2 \circ \pi^Y_2$ and therefore $f \circ \alpha_1 \circ \pi^Y_1 = f \circ \alpha_2 \circ \pi^Y_2$, so we have two maps $X \times_Y X \xrightarrow{\pi^Y_{1,2}} X_1,X_2 \xrightarrow{f\circ \alpha_{1,2}} Z$ that commute, therefore by universal property of $X \times_Z X$ we have a unique map $h: X \times_Y X \rightarrow X \times_Z X$.

However, by definition of fibered product, $X \times_Y X \xrightarrow{\pi^Y_{1,2}} X_1,X_2 \xrightarrow{\beta_{1,2}} Z$ must be valid for the universal property to be appliable. In words, maps to $X_1, X_2$ must commute in $Z$ through the maps given in $X\times_ZX$, not just any maps. Is my understanding correct? If yes, might it be the case that $f \circ \alpha_{1,2} = \beta_{1,2}$ for some reason? Or did I go in a completely wrong direction?

EDIT: I reread the exercise and it might actually be assumed that $f \circ \alpha_{1,2} = \beta_{1,2}$, or better to say, $\beta_{1,2}$ are defined as such. Here's the exercise: 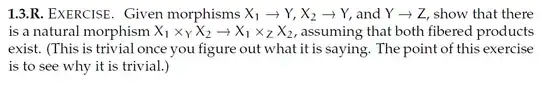enter image description here So sorry to everyone who tried with me to solve non-existent and unsolvable exercise. Maybe someone can post a counterexample to the construction in question? Otherwise the question can be closed.

Nikita Dezhic
  • 503
  • 2
    Yes, for this set-up to work one must have $\beta_i=f\alpha_i$; you can't pick any old maps for the $\beta_i$. As you show this is all category theory, there's no actual algebraic geometry here. – Angina Seng Jul 11 '20 at 08:20
  • 1
    @Angina Seng Thanks, at least that is settled, I can focus on these equalities then. Didn't understand your comment about algebraic geometry thought, there is no tag. – Nikita Dezhic Jul 11 '20 at 08:47

1 Answers1

1

The point of the exercise may have been to reinforce that a morphism to a pullback object is a pair of maps: $$ (X → A \times_C B) \quad≅\quad (X → A) ×_{(X → C)} (X → B) $$

With this, the posed problem is $``$trivial$``$: \begin{align*} X₁ ×_Y X₂ & → X₁ ×_Z X₂ & \\ \cong (X₁ ×_Y X₂ → X₁) & ×_{X₁ ×_Y X₂ → Z} (X₁ ×_Y X₂ → X₂) \end{align*}

At this point, the projections $πᵢ : X₁ ×_Y X₂ → X_i$ are two such solutions $x, y$ to the equation $f ∘ α₁ ∘ x = f ∘ α₂ ∘ y$ where both sides are of type $X₁ ×_Y X₂ → Z$, provided $f ∘ αᵢ = βᵢ$.

Musa Al-hassy
  • 2,152