Note. Edited because Adayah pointed out (correctly, and to my chagrin) that this answer was totally sloppy—sloppier even than I intended it to be. Let's hope it's better now.
When we use integration by parts on an integral
$$
\int u(x) \, \mathrm{d}v(x) = \int u(x) v'(x) \, \mathrm{d}x
$$
we implicitly treat $u$ and $v$ as parametric functions of $x$. If we plot these functions against each other on the $u$-$v$ plane, we might obtain something like the below:
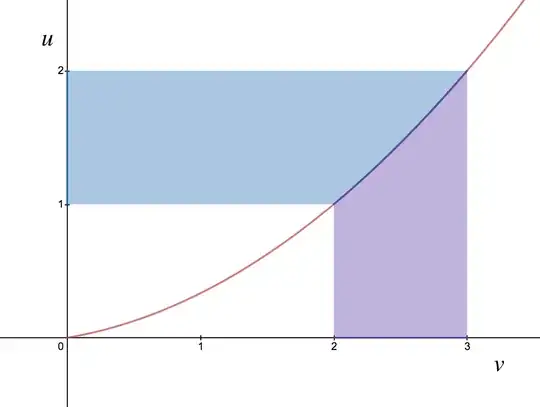
(Note that $v$ is on the horizontal axis, and $u$ on the vertical.) In this diagram, the purple region below the curve represents the definite integral
$$
\int_{v(x)=2}^3 u(x) \, \mathrm{d}v(x)
= \int_{x=v^{-1}(2)}^{v^{-1}(3)} u(x) v'(x) \, \mathrm{d}x
$$
Similarly, the blue region to the left of the curve represents the definite integral
$$
\int_{u(x)=1}^2 v(x) \, \mathrm{d}u(x)
= \int_{x=u^{-1}(1)}^{u^{-1}(2)} v(x) u'(x) \, \mathrm{d}x
$$
Note that we can set
- $x_1$ such that $u(x_1) = 1$ and $v(x_1) = 2$
- $x_2$ such that $u(x_2) = 2$ and $v(x_2) = 3$
and so we can relate those two integrals by
$$
\int_{x=x_1}^{x_2} u(x) v'(x) \, \mathrm{d}x
= \left. u(x) v(x) \phantom\int\!\!\!\!\! \right]_{x=x_1}^{x_2}
- \int_{x=x_1}^{x^2} v(x) u'(x) \, \mathrm{d}x
$$
Obviously this simple visualization of integration by parts relies (at least to some degree) on $u(x)$ and $v(x)$ being one-to-one; otherwise, we have to use signed areas. However, the necessary rigor can be added. I'm making the assumption that rigor was not what was needed here. (ETA: Though more than I provided at first!)
