9

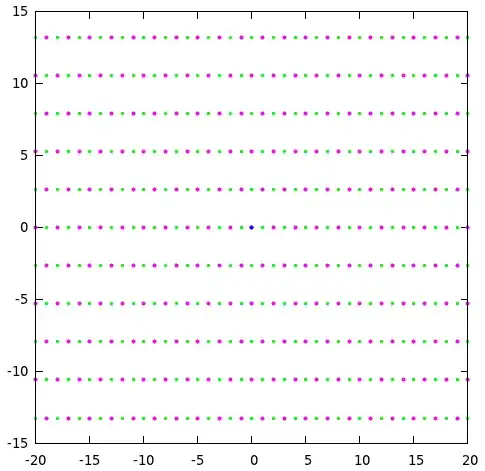
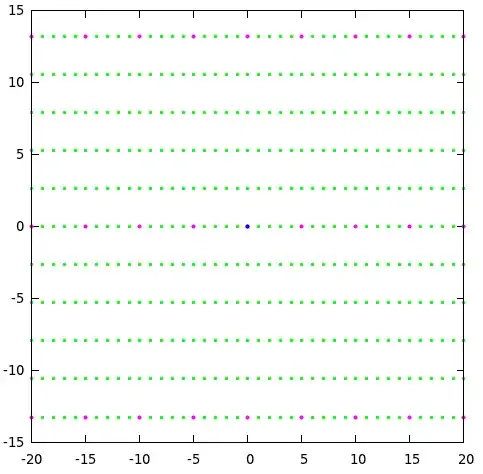
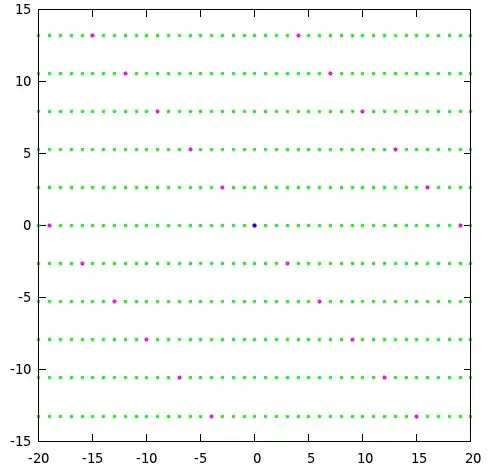
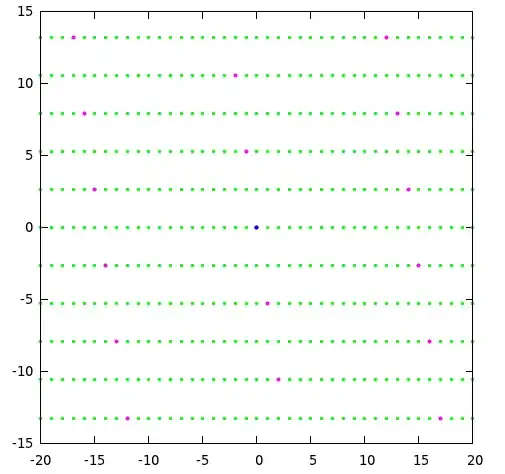
Show that the ideal $ I = (2, 1 + \sqrt{-7} ) $ in $ \mathbb{Z} [\sqrt{-7} ] $ is not principal.

My thoughts so far:

Work by contradiction. Assume that $ I $ is principal, i.e. that it is generated by some element $ z = a + b\sqrt{-7} \in \mathbb{Z}[\sqrt{-7}] $. I'm really not sure what to consider though - I can't really 'see' what $ I $ looks like.

Any help would be greatly appreciated. Thanks

user938272
  • 923

4 Answers4

9

Put $\rm\, w = 1\!+\!\sqrt{-7}.\,$ By norms $2\,$ is irreducible so, if principal $\rm\,\color{#c00}{ (2,w) = (1)}\ $ [not $(2)$ by $\rm\,2\nmid w$]

so $\rm\ 2\mid 2w,\,ww'\Rightarrow\ 2\mid (2w',ww') = \color{#c00}{(2,w)}(w') = (w'),\ $ so $\rm\ 2\mid w',\ $ contradiction. $\ \, $ QED

This is a special case of the fact that the failure of an irreducible element to be prime (or a failure of Euclid's Lemma) immediately yields a nonexistent gcd and nonprincipal ideal - see this answer.

Community
  • 1
Bill Dubuque
  • 272,048
  • When you write $w'$ you mean the conjugated? – iam_agf Dec 16 '16 at 21:06
  • 1
    @MonsieurGalois Yes, Galois should know that! $\ \ $ – Bill Dubuque Dec 16 '16 at 21:10
  • @user1952009 If you tell me what you do not understand then I will be happy to elaborate. Answers are written at different levels to accommodate readers at different levels. – Bill Dubuque Dec 16 '16 at 21:42
  • @user1952009 I offer to help you understand it and you replied with a downvote. Sheesh. You don't seem to be very sincere about desiring to understand it. That's your loss. – Bill Dubuque Dec 16 '16 at 22:28
  • I don't care understanding what you wrote, I know it is trivial, and that's the problem : you can't explain clearly something trivial (see Arturo Magidin's answer) – reuns Dec 16 '16 at 23:01
  • As you want, but the downvote is deserved, for what I took time to explain – reuns Dec 16 '16 at 23:04
  • I still don't understand why you think $(2,w) \ne (2)$ and $(2,w) \ne (1)$. You have a big problem of deduction – reuns Dec 16 '16 at 23:23
  • 1
    @user1952009 $\ $ Suppose it's principal $,(2,w) = (a).,$ Then $,a\mid 2.,$ Since $2$ is irreducible, $,a,$ is associate to $,2,$ or $,1,,$ i.e. $,(a) = (1),$ or $,(a) = (2).,$ But $,(2,w)=(a)=(2),\Rightarrow, 2\mid w,,$ contra $,w/2\not\in\Bbb Z[\sqrt{-7}].,$ Thus $,(2,w)=(a)= (1).,$ The rest of the proof is essentially Euclid's Lemma in ideal form, as explained in the linked answer. – Bill Dubuque Dec 16 '16 at 23:42
  • @reuns (formerly user1952009 ) Re-reading this a few years later, I still have no idea what you think "you explained", nor if the trivial argument in my prior comment is what you thought I "could not explain". Nor do I see any "big problem with deduction". Your remarks are among the most puzzling I've ever received on this site. – Bill Dubuque May 18 '21 at 10:03
6

Here is a picture of the elements of $\mathbb Z[\sqrt{-7}]$ (in green) embedded into the plane in such a way that their distance form the origin (blue) is equal to their norm. The ideal is drawn on top in purple.

lattices

Now here are some pictures of principal ideas.

$$(5)$$

lattice

$$(3 - \sqrt{-7})$$

lattice

$$(1 - 2\sqrt{-3})$$

lattice

$$(1 + \sqrt{-7})$$

lattice

$$(1+3\sqrt{-7},10+2\sqrt{-7})$$

lattice

You could probably see immediately that last one is not a principal ideal! The density of points is too strong for it to be principal. I am not sure how to turn this "density" concept into mathematical proof but I'm sure it can be done.

I the gnuplot command used

plot './lattice.txt' with points pointsize 0.4 pt 20 lt 2 notitle, './lattice2.txt' with points pointsize 0.5 pt 20 lt 4, './origin.txt' with points pointsize 0.5 pt 20

to draw these.

quanta
  • 12,425
4

Consider the map $N\colon\mathbb{Z}[\sqrt{-7}]\to\mathbb{Z}$ given by $$N(a+b\sqrt{-7}) = a^2+7b^2.$$ This map is multiplicative, so if $z\in\mathbb{Z}[\sqrt{-7}]$ divides $2$, then $N(z)$ divides $N(2) = 4$. So $N(z)=1$, $N(z)=2$, or $N(z)=4$. Check the possibilities, and see if any of them divides $1+\sqrt{-7}$; those are your possible generators (note that the ideal $(2,1+\sqrt{-7})$ is principal if and only if $(2,1+\sqrt{-7})=(z)$ for some $z$, which implies that $z$ divides both $2$ and $1+\sqrt{-7}$). Not check to see if any of the possible generators are actually generators.

The map $N$ is called the "norm map". It is given by taking an element of $\mathbb{Z}[\sqrt{-7}]$, and multiplying all its images under the different embeddings of its field of fractions $\mathbb{Q}(\sqrt{-7})$ into $\mathbb{C}$; it is a standard tool for studying divisibility and ideals in orders, such as $\mathbb{Z}[\sqrt{-7}]$.

Arturo Magidin
  • 398,050
  • 1
    Thanks. If $ N(\alpha) = 1 $, we are forced to have $ \alpha = 1 $. The ideal generated by $ \alpha $ is therefore the whole ring. Why can't this be the case? – user938272 May 06 '11 at 18:43
  • @user938272: Because $(2,1+\sqrt{-7})$ is not the entire ring. Verify that the square of any element in that ideal is necessarily a multiple of $2$, so the ideal cannot contain $1$. – Arturo Magidin May 06 '11 at 18:45
  • @user938272: Alternatively, notice that $(2,1+\sqrt{-7})^2 = (4,2+2\sqrt{-7},-6+2\sqrt{-7})$, so every element of the square of the ideal is a multiple of $2$, hence we cannot have $(2,1+\sqrt{-7}) = (1)$. Also: $N(\alpha)=1$ implies $\alpha=\pm 1$, and not only $\alpha=1$. – Arturo Magidin May 06 '11 at 19:05
0

To prove this note that $1 \not \in I$ so $I \not = (1)$. Then suppose $I = (\alpha)$, that implies that $\alpha = 2$ or $\alpha = 1 + \sqrt{-7}$ since those are both irreducibles, but neither of them can hold since one irreducible is not a multiple of another.

quanta
  • 12,425