What is the geometric interpretation of the transpose?

Question

I can follow the definition of the transpose algebraically, i.e. as a reflection of a matrix across its diagonal, or in terms of dual spaces, but I lack any sort of geometric understanding of the transpose, or even symmetric matrices.

For example, if I have a linear transformation, say on the plane, my intuition is to visualize it as some linear distortion of the plane via scaling and rotation. I do not know how this distortion compares to the distortion that results from applying the transpose, or what one can say if the linear transformation is symmetric. Geometrically, why might we expect orthogonal matrices to be combinations of rotations and reflections?

Answer 1

To answer your second question first: an orthogonal matrix $O$ satisfies $O^TO=I$, so $\det(O^TO)=(\det O)^2=1$, and hence $\det O = \pm 1$. The determinant of a matrix tells you by what factor the (signed) volume of a parallelipiped is multipled when you apply the matrix to its edges; therefore hitting a volume in $\mathbb{R}^n$ with an orthogonal matrix either leaves the volume unchanged (so it is a rotation) or multiplies it by $-1$ (so it is a reflection).

To answer your first question: the action of a matrix $A$ can be neatly expressed via its singular value decomposition, $A=U\Lambda V^T$, where $U$, $V$ are orthogonal matrices and $\Lambda$ is a matrix with non-negative values along the diagonal (nb. this makes sense even if $A$ is not square!) The values on the diagonal of $\Lambda$ are called the singular values of $A$, and if $A$ is square and symmetric they will be the absolute values of the eigenvalues.

The way to think about this is that the action of $A$ is first to rotate/reflect to a new basis, then scale along the directions of your new (intermediate) basis, before a final rotation/reflection.

With this in mind, notice that $A^T=V\Lambda^T U^T$, so the action of $A^T$ is to perform the inverse of the final rotation, then scale the new shape along the canonical unit directions, and then apply the inverse of the original rotation.

Furthermore, when $A$ is symmetric, $A=A^T\implies V\Lambda^T U^T = U\Lambda V^T \implies U = V $, therefore the action of a symmetric matrix can be regarded as a rotation to a new basis, then scaling in this new basis, and finally rotating back to the first basis.

Answer 2

yoyo has succinctly described my intuition for orthogonal transformations in the comments: from polarization you know that you can recover the inner product from the norm and vice versa, so knowing that a linear transformation preserves the inner product ($\langle x, y \rangle = \langle Ax, Ay \rangle$) is equivalent to knowing that it preserves the norm, hence the orthogonal transformations are precisely the linear isometries.

I'm a little puzzled by your comment about rotations and reflections because for me a rotation is, by definition, an orthogonal transformation of determinant $1$. (I say this not because I like to dogmatically stick to definitions over intuition but because this definition is elegant, succinct, and agrees with my intuition.) So what intuitive definition of a rotation are you working with here?

As for the transpose and symmetric matrices in general, my intuition here is not geometric. First, here is a comment which may or may not help you. If $A$ is, say, a stochastic matrix describing the transitions in some Markov chain, then $A^T$ is the matrix describing what happens if you run all of those transitions backwards. Note that this is not at all the same thing as inverting the matrix in general.

A slightly less naive comment is that the transpose is a special case of a structure called a dagger category, which is a category in which every morphism $f : A \to B$ has a dagger $f^{\dagger} : B \to A$ (here the adjoint). The example we're dealing with here is implicitly the dagger category of Hilbert spaces, which is relevant to quantum mechanics, but there's another dagger category relevant to a different part of physics: the $3$-cobordism category describes how space can change with time in relativity, and here the dagger corresponds to just flipping a cobordism upside-down. (Note the similarity to the Markov chain example.) Since relativity and quantum mechanics are both supposed to describe the time evolution of physical systems, it's natural to ask for ways to relate the two dagger categories I just described, and this is (roughly) part of topological quantum field theory.

The punchline is that for me, "adjoint" is intuitively "time reversal." (Unfortunately, what this has to do with self-adjoint operators as observables in quantum mechanics I'm not sure.)

Answer 3

Overview If a matrix A acting on vectors tells you how a vector is transformed, the matrix $A^T$ tells you how linear measurement of this vector are transformed.

If E is your vector space, the "space of linear measurements", or dual space is the space of all linear transformation $E \rightarrow \mathbb{R}$. Said differently, it is the space of all linear functions that take in a vector and output a number.

Example Let's work in $\mathbb{R}^2$.

• We have a generic vector $X = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$
• A sample matrix $A = $$ \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} $
• A sample linear measurement $h(X)=2x_1$, we note it $\begin{pmatrix} 2 \\ 0 \end{pmatrix}$

Maybe this measurement has some meaning physically (total mass or momentum...). We want to know how the transformation A affects h.

The familiar product $AX = \begin{pmatrix} x_1 + x_2 \\ x_2 \end{pmatrix}$ tells you how X is transformed. Now that we have seen that X has changed we might ask, what is the new measurement of X by h? It is obtained by computing $h(AX)$:

$h(Ax) = h(\begin{pmatrix} x_1 + x_2 \\ x_2 \end{pmatrix}) = 2x_1 + 2x_2$ which we note as $\begin{pmatrix} 2 \\ 2 \end{pmatrix}$

So when we transform by A, h goes from $\begin{pmatrix} 2 \\ 0 \end{pmatrix}$ to $\begin{pmatrix} 2 \\ 2 \end{pmatrix}$

It turns out that this transformation is precisely what the transpose is doing, as you can verify: $A^T\begin{pmatrix} 2 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 2 \end{pmatrix}$

This is kind of hand-wavy, if you want more details look up dual space, which makes all of this precise.

Answer 4

We better interpret the geometric meaning of transpose from the view point of projective geometry. Because only in projective geometry, it is possible to interpret that of all square matrices.

It would be difficult for OP to understand and grasp the necessary premises or mathematical basis when interpreting the meaning in projective geometry of a square matrix's transpose only from a not too much lengthy answer posted here. So I would recommend you to read the article in this link first.

After read article in the above link, use the basic principles below:

1. Some basic or elementary geometric transformations are equivalent to Househodler's elementary matrices in homogeneous coordinates in projective geometry; that is what stereohomology is defined;

2. All square matrices can be represented by concatenated multiplication of elementary matrices;

3. a transpose of any elementary geometric transformation means exchanging the "center" and the "interface" of it per the definition of stereohomology.

then: the transpose of any square matrices have their own geometric meaning in projective geometry, though for complicated cases, the geometric interpretation of transpose might not be unique.

Answer 5

To get a geometric intuition of matrix transposition, I build upon my geometric intuition of the dot product.

The dot product seen as a projection One geometric intuition behind the dot product $a \cdot b$ of two vectors is to see it as follow : you first project the first vector $a$ on the second vector $b$, and then you multiply the norm of this projection by the length of the vector $b$.

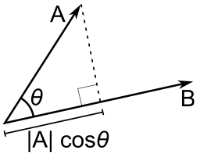
But since the dot product is commutative, that is $a \cdot b = b \cdot a$, you can also see it as the multiplication of the length of $a$ with the length of the projection of the second vector $b$ on the first vector $a$ (you just need to mentally exchange $a$ and $b$ in the previous drawing).

So when you think of the dot product as a projection, there are $2$ ways to do it : either you project the first vector on the second, or you project the second vector on the first.

Link between transposition and dot product Let $M$ be some $m$ by $n$ matrix, $a$ a vector of length $n$ and $b$ a vector of length $m$. Let's try to find a matrix a $n$ by $m$ matrix $X$ such that: $$Ma \cdot b = X b \cdot a $$

There is only one solution to this equation, which is $X = M^T$. Let's interpret this geometrically.

The left part of this equality can be geometrically interpreted as follow :

1. Apply the linear transformation $M$ to the vector $a$
2. Project the result of this transformation on the vector $b$
3. Multiply the length of this projection by the length of $b$

The right part does the exact same thing, but by projecting $b$ on $a$ :

1. Apply some linear transformation $X$ to the vector $b$
2. Project the result of this transformation on the vector $a$
3. Multiply the length of this projection by the length of $a$

And this is where a geometric intuition comes in : if I have some transformation $M$ and I want to intuitively guess what will be its transposition, here are the steps I follow :

1. I picture two vectors $a$ and $b$, just as in the above drawing
2. I apply mentally apply $M$ that transformation to the vector $a$ and see how the projection (the "shadow") of the vector $a$ behaves.
3. I fix the vector $a$ and now I try to move the vector $b$ in such a way that the length of the projection of $b$ on the vector $a$ behaves the same way as the projection of $a$ on $b$.
4. If I can find such a transformation of $b$ that matches these requirements, it must be $M^T$ !

Let's apply this with rotations !

Time for intuition training ! Let's intuitively guess what the transposition of a rotation should be by following the previous steps :

1. Picture two vectors $a$ and $b$ like the picture above
2. Rotate the vector $a$ by some angle $\phi$ smaller than $\theta$ towards the vector $b$. The length of the projection increases.
3. Now instead of rotating $a$, rotate the vector $b$ by the same angle $\phi$. This should rotate $b$ away from the vector $a$. Also the length of the projection of $b$ on $a$ decreases. So this is not what we want ...
4. Let's try to rotate $b$ in the other direction, that is towards the vector $a$. Now the projection increases. It looks like the rotation $-\phi$ should give us what we want.

And this is indeed the case !

Now you can try that thought experiment for other kinds of transformations. It's not always easy, but it's rewarding, because the transposition is way more than just a diagonal symmetry on a grid of numbers !