If $P$ is false, and $Q$ is true, then why does $P \implies Q$?

Question

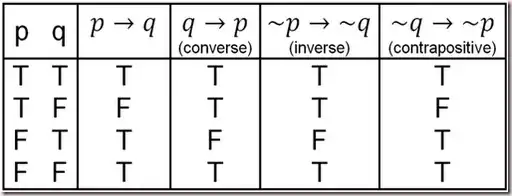
I have often seen truth tables similar to this one:

The first two rows, where $P$ is true, make sense to me. However, why does $P$ being true and $Q$ being false mean that $P \implies Q$?

To make the question clearer to myself, I came up with the following example: let $P$ be whether or not it is raining. Let Q be whether or not I am wearing a coat. Then, there are $4$ possibilities:

It is raining; I am wearing a coat.
It is raining; I am not wearing a coat.
It is not raining; I am wearing a coat.
It is not raining; I am not wearing a coat.

$P \implies Q$ is the same as saying if it is raining, then I will wear a coat. This statement says nothing about what happens when it is not raining. Therefore, why do we say not raining $\implies$ coat?

You can look here for a good explanation for what regards material implication — Tortar, Jun 28 '20 at 10:25

score 1 · Accepted Answer · answered Jun 28 '20 at 10:37

1

The reason is that, in mathematics, "$P \implies Q$" is equivalent to "$Q$ or not $P$". Thus if $Q$ is true, $Q$ or not $P$ is also true, whatever $P$ is.

answered Jun 28 '20 at 10:37

J.-E. Pin

40,163

score 0 · Answer 2 · answered Jun 28 '20 at 10:28

Because you can wear a coat when it's not raining, for example when it's snowing.

More generally, $P$ has an influence on the state of $Q$, not the other way around, which is why the arrow is shown in one way only. If you consider a two-way relation, for example $P \iff Q$, then both have an influence on the state of the other. For example when $P$ denotes eating no meat and $Q$ denotes being a vegetarian (although one might find easier examples).

If $P$ is false, and $Q$ is true, then why does $P \implies Q$?

2 Answers2