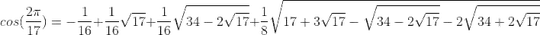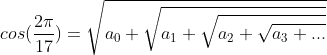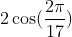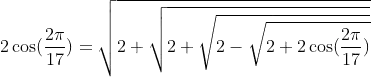5

From another math.stackexchange.com question we have

enter image description here

Can this expression be written as a nested square root only? ie,

enter image description here

where all of the a's are integers?

Edit: From the comment, it seems that it may be more interesting to look at

enter image description here

After doing some more research, I found that

enter image description here

This was based on this answer to a related question.. So it appears that it would be possible with an infinite nested square root. How about a finite nested square root? Would that be possible?

Anton Vrdoljak
  • 2,717
No One in Particular
  • 195
  • The obvious quick answer is that No. This is not possible. The reason is that if $a_0,a_1,\ldots, a_n$ are all integers, then the nested square root is an algebraic integer. But $\cos(2\pi/17)$ is not an algebraic integer. On the other hand, $$2\cos(2\pi/17)=\zeta_{17}+\zeta_{17}^{-1}$$ is an algebraic integer as a sum of twoalgebraic integers (this time complex roots of unity). Therefore a much more interesting question is whether $2\cos(2\pi/17)$ is a nested square root of integer terms. Could you please edit the question to make it more interesting? – Jyrki Lahtonen Jun 27 '20 at 15:52

1 Answers1

2

For all $A$ and $a_i$ it follows: $$A=\sqrt{1+a_1(A+1)+(A-a_1-1)\sqrt{1+a_2(A+2)+(A-a_2)\sqrt{1+a_3(A+3)+\cdots}}}$$

Let $$A=\cos \bigg(\frac{2\pi}{17}\bigg)$$ and let $$a_i=\frac{1}{A+i}$$ then, if $B_n=A-a_n+n-2$, we have

$$\cos\bigg(\frac{2\pi}{17}\bigg)=\sqrt{2+B_1\sqrt{2+B_2\sqrt{2+B_3\sqrt{2+\cdots}}}}$$

Any number cna be expressed as an infinite-nested radical, but given that $\cos(2\pi/17)$ is pretty obscure, I think this formula is the best to apply, since it works with infinite parameters and is not periodic (making it interesting!).

Here is an interesting one for cubed root (but periodic). Note that $$\color{red}{\cos\bigg(\frac{2\pi}{17}\bigg)}^3=\frac 14\cos \bigg(\frac{6\pi}{17}\bigg)+\frac 34\color{red}{\cos\bigg(\frac{2\pi}{17}\bigg)}$$

thus

$$\cos \frac{2\pi}{17}=\sqrt[3]{\frac 14\cos \bigg(\frac{6\pi}{17}\bigg) +\frac 34\sqrt[3]{\frac 14\cos \bigg(\frac{6\pi}{17}\bigg) +\frac 34\sqrt[3]{\frac 14\cos \bigg(\frac{6\pi}{17}\bigg) +\cdots}}}$$

Mr Pie
  • 9,459
  • Can all of the Bs be integers? This is what I was looking for. (Sorry that I didn't specify it correctly.) – No One in Particular Jun 27 '20 at 15:42
  • @NoOneinParticular None of $B_n$ can be an integer since $n>0$ is a whole number. Radical equations and trigonometry go hand-in-hand (see here) but they most often revolve around "units", roots of numbers that neaten results and yield most elegant ones. e.g. $$\cos\bigg(\frac{2\pi}5\bigg)=\frac 12\sqrt{2-\sqrt{2+\sqrt{2-\sqrt{2+\cdots}}}}$$ because the denominator $5$ makes a good unit for radicals (e.g. $a+b\sqrt 5$ forms work in wonderful ways). $17$ is rather obscure, so less elegant radicals in consequence. – Mr Pie Jun 27 '20 at 16:01
  • I have generalised the method to solve your question – Sivakumar Krishnamoorthi Sep 14 '20 at 00:50