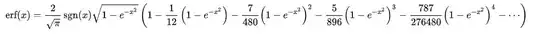Confused about Burmann series coefficients to approximate $erf(x)$

Question

I've been looking into Burmann series to approximate special functions. I looked at "On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion". Looking at the example for $erf$ also shown here Integration of $e^{-x^2}$ the authors create a new type of constant called $c_i$ and somehow come up with $c0 = \sqrt{\pi}/2 $

where (32) is

and

I don't understand what these constants are. They appear to be unrelated to Burmann constants in the corresponding burrman series, but some how a retraction of

How can I get the rest of the constants?

Answer 1

I will be frank, I have no idea what they refer to when deriving the coefficients as the text is unclear. The closest interpretation of

For example, using only $c_1$ and requesting the correct slope at $z = 0$, one gets an approximation of the error function with a relative error smaller than $1.2\%$.

that I have is that they tried to have

$$f(z)=\frac{2\operatorname{sign}(z)}{\sqrt\pi}\sqrt{1-e^{-z^2}}\left(\frac{\sqrt\pi}2+c_1e^{-z^2}\right)$$

satisfy

$$f'(0)=\operatorname{erf}'(0)$$

and that they did similar for $c_2$ by trying to match the third derivative as well (the even order derivatives are vanishing at the origin). This however leads me to get

$$\frac{2\operatorname{sign}(z)}{\sqrt\pi}\sqrt{1-e^{-z^2}}\left(\frac{\sqrt\pi}2+\left(\frac{23}{12}-\sqrt\pi\right)e^{-z^2}+\left(\frac{\sqrt\pi}2-\frac{11}{12}\right)e^{-2z^2}\right)$$

which is completely different from their solution.

Indeed one can easily verify their solution does not match the first derivative.

What really boggles me is how good the result is, and without any involvement with $\pi$. I don't see what kinds of conditions might yield such a result.