-1

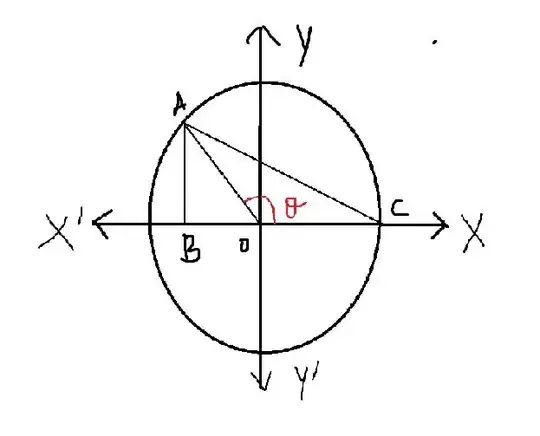
enter image description here

In this figure how can we find out geometrically that the sine of the angle $\theta$ = $AB /AO$ without using the equation sin (180 - $\theta$) = sin ($\theta$)

Akash Arjun
  • 328
  • What sort of answer are you looking for? It just… is. Set $c = 1$ WLOG; then as $A$ traverses round the circle, the y-value of $A$ is always equal to $\sin \theta$. One could say that this is how $\sin$ is defined. How exactly are you defining $\sin$? – Patrick Stevens Jun 20 '20 at 10:47
  • Use $\sin (\theta)=\cos(\frac{\pi}{2}-\theta)$ – UmbQbify Jun 20 '20 at 10:50
  • I was taught that sin of an angle( in a right-angled triangle) is the ratio of the length of the opposite side to its hypotenuse. So I mean to ask that when the angle is obtuse why do I take out its sine using the above method? @ Patrick Stevens – Akash Arjun Jun 20 '20 at 10:55
  • @ AshWhole Can you please tell me how to use that fact to arrive at a conclusion – Akash Arjun Jun 20 '20 at 10:57
  • Find the $\angle BAO$ . – UmbQbify Jun 20 '20 at 10:59
  • @ AshWhole that gives me 90 + $\theta$ . But that does not help me as I want to solve the question geometrically – Akash Arjun Jun 20 '20 at 11:03
  • Just define that $\sin\theta=\frac{AB}{AO}$ where $AB$ is the $y$- coordinate of the point $A$. Observe that in your definition of sine the function is defined only for values $0<\theta<\frac\pi2$. – user Jun 20 '20 at 11:13
  • 1
    @AkashArjun: You might be interested in this answer. – Blue Jun 20 '20 at 19:38

1 Answers1

0

"The definition of sin of and angle is opposite/hypotenuse" - well that only works for a right-angled triangle, and is the beginning of the definition of the sine function.

In order to extend the definition draw a unit circle with centre at the origin. Measure the angle counterclockwise from the positive x-axis and take a point (x,y) on the circle. The sine of the angle (equivalent to opposite/hypotenuse in the first quadrant, with the hypotenuse made equal to 1) is y and the cosine of the angle is x. You can go round the circle more than once, so you can see that the functions are periodic.

This is why the functions are sometimes known as circular functions and underlies why they come in so surprisingly useful.

Akash Arjun
  • 328