To show this, I have used definitions for $\cos(x)$ and $\sin(x)$: $$x\cdot \cos(x)+1/2\sin(x)=x\cdot \sum_{n=0}^\infty \frac{(-1)^n}{(2n)!}\cdot x^{2n}+1/2\cdot \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}\cdot x^{2n+1}$$
However, i do not how I'm supposed to proceed from here. You've got any ideas? This comes from the fourier series of $x\cdot \cos(x)$. We have the fourier coefficients as: $$ c_{-1}=-\frac{i}4, c_0=0,c_1=\frac{i}4$$ and $$c_n=(-1)^{n-1} \cdot \frac{in}{n^2-1}$$ when $|n|\geq 2$
Hint:
$$\dfrac{2n\sin nx}{(n+1)(n-1)}=\dfrac{\sin nx}{n-1}-\dfrac{\sin nx}{n+1}$$
Now $(-1)^n\dfrac{\sin nx}{n-1}$ is the imaginary part of $$\dfrac{(-1)^ne^{inx}}{n-1}=e^{ix}\cdot-\dfrac{(-e^{ix})^{n-1}}{n-1}$$
Now $$\sum_{n=2}^\infty-\dfrac{(-e^{ix})^{n-1}}{n-1}=\ln(1+e^{ix})=\ln (e^{ix/2})+\ln\left(2\cos\dfrac x2\right)=(2n\pi+\dfrac x2)i+\ln\left(2\cos\dfrac x2\right)$$
Put $n=0$ to find the principal value
Similarly for $$\dfrac{\sin nx}{n+1}$$
Finally use How to prove Euler's formula: $e^{i\varphi}=\cos(\varphi) +i\sin(\varphi)$?
$x\cos(x)$ is a continuous and odd function, so its Fourier series over $(-\pi,\pi)$ only has sine terms. $$ \int_{-\pi}^{\pi}x\cos(x)\sin(nx)\,dx=\frac{1}{2}\int_{-\pi}^{\pi}x\sin\left(\left(n+\tfrac{1}{2}\right)x\right)\,dx+\frac{1}{2}\int_{-\pi}^{\pi}x\sin\left(\left(n-\tfrac{1}{2}\right)x\right)\,dx $$ and $$ \int_{-\pi}^{\pi}x\sin(mx)\,dx\stackrel{\text{IBP}}{=}\frac{1}{m}\left[-x\cos(mx)\right]_{-\pi}^{\pi}-\frac{1}{m}\int_{-\pi}^{\pi}\cos(mx)\,dx $$ leads to $ \int_{-\pi}^{\pi}x\cos(x)\sin(x)\,dx = -\frac{\pi}{2} $ and $$ \int_{-\pi}^{\pi}x\cos(x)\sin(nx)\,dx = \frac{2\pi n}{n^2-1}(-1)^n $$ for any $n\geq 1$. 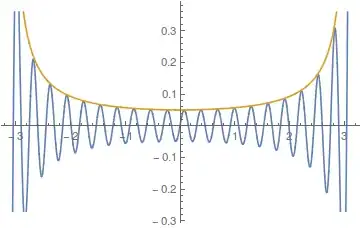This gives $$ x\cos(x)+\frac{\sin(x)}{2}\stackrel{L^2(-\pi,\pi)}{=}\sum_{n\geq 2}\frac{2n(-1)^n}{n^2-1}\sin(nx) $$ with pointwise convergence in $(-\pi,\pi)$ and uniform convergence over any compact subset of $(-\pi,\pi)$, like in the case $$ \frac{\pi-x}{2}\stackrel{L^2(0,2\pi)}{=}\sum_{n\geq 1}\frac{\sin(nx)}{n}.$$ Here the partial sum up to $n=20$ compared with the actual function:
and the error compared to $\frac{1}{20\cos(x/2)}$:
