$$P\left(Z\le z\right)=P\left(\left|X-Y\right|\le z\right)=P\left(-z\le X-Y\le z\right)=P\left(Y-z\le X\le Y+z\right)$$
This means that, because $\space f(x,y)=f(x)f(y) \space$ as they are independent, we get to calculate this integral:
$$\int _0^{\infty }\:\int _{y-z}^{y+z}\:\left(\lambda e^{-\lambda x}\right)^2dxdy$$
We get
$$\left(e^{\left(-2\cdot \lambda \cdot z\right)}\cdot \left(e^{\left(4\cdot \lambda \cdot z\right)}-1\right)\right)/4$$
Which is not what we want
So where's the mistake?
The main error arises from not considering when the interval $[y-z, y+z]$ is not a subset of $[0,\infty)$. That is to say, when $y < z$, then $y-z < 0$. So you need to take this into account when integrating over $x$. The second error is in writing the integrand as the square of the marginal density $f_X(x)$, when the outer integral is with respect to $y$.
The way to set up the integral is
$$\begin{align*} &\Pr[Y - z \le X \le Y + z] \\ &\quad = \int_{y=0}^z \int_{x=0}^{y+z} f_{X \mid Y}(x \mid y) f_Y(y) \, dx \, dy + \int_{y=z}^\infty \int_{x=y-z}^{y+z} f_{X \mid Y}(x \mid y) f_Y(y) \, dx \, dy\end{align*}$$ where $f_{X \mid Y}(x \mid y) = f_X(x)$ because $X$ and $Y$ are independent.
As the above is not sufficiently detailed for the audience, I will proceed with a full explanation as follows.
Note we want to compute $\Pr[Y - z \le X \le Y + z]$ for IID $$X, Y \sim \operatorname{Exponential}(\lambda)$$ with rate parametrization $$f_X(x) = \lambda e^{-\lambda x}, \quad x \ge 0, \\ f_Y(y) = \lambda e^{-\lambda y}, \quad y \ge 0.$$ We will do this the mechanical way as requested, then show an alternative computation that is easier. First note $$\begin{align*} &\Pr[Y - z \le X \le Y + z] \\ &= \Pr[0 \le X \le Y+z \mid Y \le z]\Pr[Y \le z] + \Pr[Y - z \le X \le Y + z \mid Y > z]\Pr[Y > z], \end{align*}$$ where we conditioned the probability on the event $Y > z$. This gives us the aforementioned sum of double integrals.
Next, we consider the following idea: let $$f_{X,Y}(x,y) = f_X(x) f_Y(y) = \lambda^2 e^{-\lambda (x+y)}, \quad x, y \ge 0$$ be the joint density. We want to compute $F_Z(z) = \Pr[|X - Y| \le z]$. To do this, we want to integrate the joint density over the region for which $|X - Y| \le z$, when $X, Y \ge 0$; i.e., when $(X,Y)$ is in the first quadrant of the $(X,Y)$ coordinate plane. Notably, when $Y = X$, then $|X-Y| = 0$, and as the distance away from this line increases, $|X-Y|$ increases. So this region comprises a "strip" of width $\sqrt{2} z$ centered over $Y = X$ in the first quadrant. We can also see this by simply sketching the region bounded by the lines $X \ge 0$, $Y \ge 0$, $Y \le X+z$, $Y \ge X-z$.
But because this region is symmetric about $Y = X$, and the joint density is also symmetric about this line, the integral can be written symmetrically: $$\int_{x=0}^\infty \int_{y=x}^{x+z} f_{X,Y}(x,y) \, dy \, dx + \int_{y=0}^\infty \int_{x=y}^{y+z} f_{X,Y}(x,y) \, dx \, dy,$$ and these two pieces are equal in value. This avoids the computation of two separate double integrals with different values.
To really solidify the point, here are some diagrams of the regions of integration. The region described in the first setup looks like this:
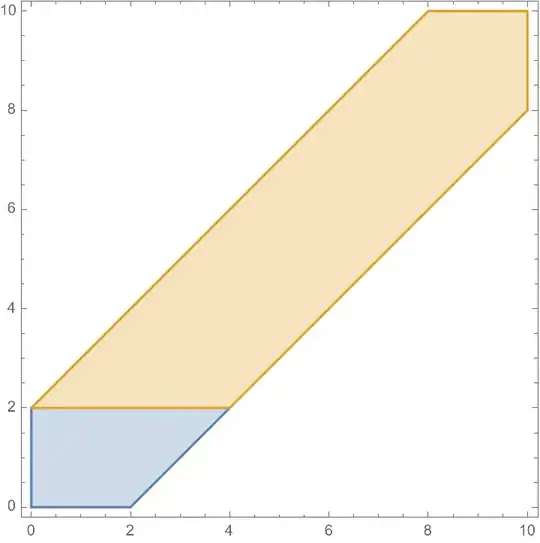The blue region is the first integral, and the orange is the second (where I've only plotted up to $x, y \le 10$ since obviously a plot to $\infty$ is not possible), for the choice $z = 2$. This illustrates why we must split the region into two parts, because if we integrated $x$ on $[y-z, y+z]$ for the blue region, you'd be including a portion in the second quadrant that is not allowed. But this is not the only way to split up the region:
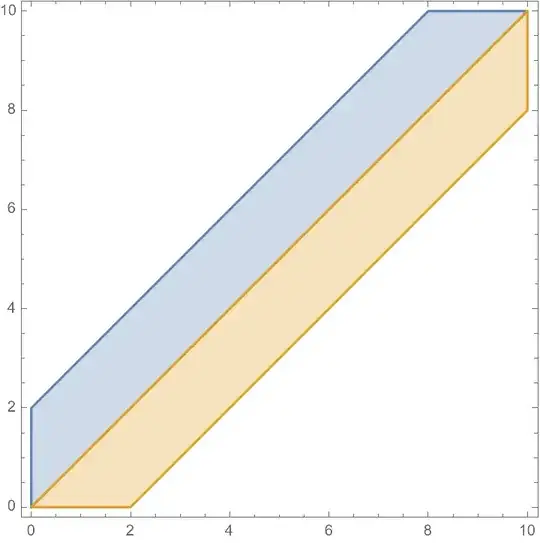This is the second approach I described. The blue region is the first integral, and the orange region is the second. This is possible because the order of integration of one integral is the reverse of the order in the other, whereas in the first setup, the order of integration is the same (horizontal strips). Here, we integrate the blue region in vertical strips, and the orange region in horizontal strips. And because of the symmetry, we don't even have to compute both--the contribution of the orange region is equal to the contribution of the blue.
As mentioned in another answer, you get problems with negative values (you cannot consider $y-z \le 0$ in yur duble integral, for example). We can solve the problem as follows. Consider \begin{align} P(X\le Y\text{ and }Y-X\le z)={}&P(X\le Y\text{ and }Y\le X + z)\\ ={}&\int_0^\infty dx\,\lambda e^{-\lambda x}\int_x^{x+z}dy\,\lambda e^{-\lambda y}\\ ={}&\int_0^\infty dx\,\lambda e^{-\lambda x}\left(e^{-\lambda x} - e^{-\lambda(x+z)}\right)\\ ={}&\int_0^\infty dx\,\lambda e^{-2\lambda x}\left(1 - e^{-\lambda z}\right)\\ ={}&\frac{1}{2}\left(1 - e^{-\lambda z}\right) \end{align} where in the second line we used independence. by symmetry (and the fact that the exponential distribution has no atoms): $$P(Z\le z) = P(X\le Y\text{ and }Y-X\le z) + P(Y\le X\text{ and }X-Y\le z) = 1 - e^{-\lambda z}.$$ Differentiating we get $f_Z(z) = \lambda e^{-\lambda z}$.
There are probably neater ways to solve this, let me know if you find any.
Since @heropup has found the mistake, I'll join @DanielRobertNicoud in finding the distribution another way. Since $X$ has characteristic function $\frac{1}{1-it/\lambda}$, $W:=X-Y$ has characteristic function$$\frac{1}{1+t^2/\lambda^2}=\frac12\left(\frac{1}{1-it/\lambda}+\frac{1}{1+it/\lambda}\right)$$and PDF$$\frac12(\lambda e^{-\lambda w}[w\ge0]+\lambda e^{\lambda w}[w<0])=\lambda e^{-\lambda|w|}.$$So $Z$ has PDF$$\frac12[z\ge0]\left(\lambda e^{-\lambda|z|}+\lambda e^{-\lambda|-z|}\right)=\lambda e^{-\lambda z}[z\ge0],$$as required.
